Probability

General

An outcome $s$ is in sample space $S$

$$
\begin{align}
s &\in S \\
S &= \set{s_0, s_1, s_2, \dots}
\end{align}
$$

An event $E$ is a subset of samples in the sample space

$$
\begin{align}
E \subset S
\end{align}
$$

A Probability is a mapping of an event to a number that indicates how likely that event is to occur. Some Axioms:

1. For any event $A$, $P(A) \ge 0$
2. $P(S) = 1$
3. If events $A_1, A_2, \dots$ are disjoint ($\forall A_i, A_j : A_i \cup A_j = \emptyset$) then $P(A_1 \cup A_2 \cup \dots) = P(A_1) + P(A_2) + \dots $

Conditional Probability

https://www.probabilitycourse.com/chapter1/1_4_0_conditional_probability.php

$$
\begin{align}
P(A|B) &= \frac{P(A \cap B)}{P(B)}
\end{align}
$$

Note that

1. $A \cap B = 0 \implies P(A|B) = 0$
2. $A \subset B \implies P(A \cap B) = P(A) \implies P(A|B) = \frac{P(A)}{P(B)}$
3. $B \subset A \implies P(A \cap B) = P(B) \implies P(A|B) = 1$

Chain Rule

$$
\begin{align}
P(A|B) &= \frac{P(A \cap B)}{P(B)} \\
P(B|A) &= \frac{P(A \cap B)}{P(A)} \\
\\
P(A \cap B) &= P(A|B) P(B) = P(B|A) P(A) \\
\end{align}
$$

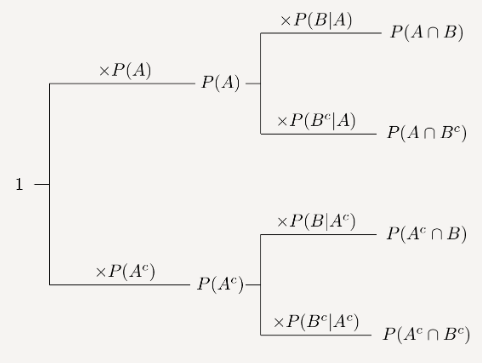
Independence

$$
\begin{align}
A, B \text{ are independent} &\iff P(A \cap B) = P(A) P(B) \\
\\
P(A|B) &= \frac{P(A \cap B)}{P(B)} \\
P(A|B) &= \frac{P(A)P(B)}{P(B)} \\
P(A|B) &= P(A) \\
\end{align}
$$

Random Variables

A random variable $X$ is a mapping from specific outcomes to the real number line

$$
\begin{align}
X : S \rightarrow \mathbb{R}
\end{align}
$$

Note that a random variable is a function, but is often treated/notated as a scalar.

A random variable will have a Range, or a set of possible values for $X$.

$$
\begin{align}
Range[X] &= R_X \\
R_X &= \set{x_i | \exists s \in S: X(s) = x_i} \\
R_X &= \set{x_0, x_1, x_2, \dots} \\
\end{align}
$$

Expectation

https://www.probabilitycourse.com/chapter3/3_2_2_expectation.php

$$
\begin{align}
E[X] &= \sum_{x_k \in R_X} x_k P_X(x_k) \\
E[X] &= \mu_X \\
\end{align}
$$

Linearity of Expectation

$$
\begin{align}
E[aX + b] &= \sum_{x_k \in R_X} (a x_k + b) P_X(x_k) &&& a, b \in \mathbb{R} \\
E[aX + b] &= \sum_{x_k \in R_X} a x_k P_X(x_k) + \sum_{x_k \in R_X} b P_X(x_k) &&& a, b \in \mathbb{R} \\
E[aX + b] &= a \sum_{x_k \in R_X} x_k P_X(x_k) + b \sum_{x_k \in R_X} P_X(x_k) &&& a, b \in \mathbb{R} \\
E[aX + b] &= a E[X] + b &&& a, b \in \mathbb{R} \\
\end{align}
$$

Variance

$$
\begin{align}
Var[X] &= E[ (X – \mu_X)^2] \\
Var[X] &= \sum_{x_k \in R_X} (x_k – \mu_X)^2 P_X(x_k) \\
\end{align}
$$

Alternatively, it is common to express Variance as

$$
\begin{align}
Var[X] &= \sum_{x_k \in R_X} (x_k – \mu_X) (x_k – \mu_X) P_X(x_k) \\

Var[X] &= \sum_{x_k \in R_X} (x_k^2 – 2 \mu_X x_k + \mu_X^2) P_X(x_k) \\

Var[X] &= \sum_{x_k \in R_X} x_k^2 P_X(x_k) – 2 \mu_X \sum_{x_k \in R_X} x_k P_X(x_k) + \mu_X^2 \sum_{x_k \in R_X} P_X(x_k) \\

Var[X] &= \sum_{x_k \in R_X} x_k^2 P_X(x_k) – 2 \mu_X \mu_X + \mu_X^2 \\

Var[X] &= \sum_{x_k \in R_X} x_k^2 P_X(x_k) – 2 \mu_X^2 + \mu_X^2 \\

Var[X] &= \sum_{x_k \in R_X} x_k^2 P_X(x_k) – \mu_X^2 \\

Var[X] &= E[X^2] – \mu_X^2 \\

\end{align}
$$

Nonlinearity of Variance

$$
\begin{align}
Var[aX + b] &= \sum_{x_k \in R_X} \{ a x_k + b – E[aX + b] \}^2 P_X(x_k) &&&a, b \in \mathbb{R} \\
Var[aX + b] &= \sum_{x_k \in R_X} \{ a x_k + b – (a E[X] + b) \}^2 P_X(x_k) \\
Var[aX + b] &= \sum_{x_k \in R_X} \{ a (x_k – E[X]) \}^2 P_X(x_k) \\
Var[aX + b] &= a^2 \sum_{x_k \in R_X} (x_k – E[X])^2 P_X(x_k) \\
Var[aX + b] &= a^2 Var[X] \\
\end{align}
$$