Consider the second order system where the input and output are described by
$$
\begin{align}
a_2 \frac{d^2 y(t)}{dt^2} + a_1 \frac{d y(t)}{dt} + a_0 y(t) &= b_1 \frac{d x(t)}{dt} + b_0 x(t) \\
\end{align}
$$
Using the differentiation property, we can take the Laplace transform of both sides to get
$$
\begin{align}
a_2 s^2 Y(s) + a_1 s Y(s) + a_0 Y(s) &= b_1 s X(s) + b_0 X(s) \\
(a_2 s^2 + a_1 s + a_0) Y(s) &= (b_1 s + b_0) X(s) \\
\end{align}
$$
Recall from the Convolution property that the benefit of using Transforms is to describe the output using the impulse response
$$
\begin{align}
Y(s) &= H(s) X(s) \\
H(s) &= \frac{Y(s)}{X(s)} \\
\end{align}
$$
We can rearrange the Laplace Transform above to determine $H(s)$.
$$
\begin{align}
\frac{Y(s)}{X(s)} &= \frac{b_1 s + b_0}{a_2 s^2 + a_1 s + a_0} \\
H(s) &= \frac{b_1 s + b_0}{a_2 s^2 + a_1 s + a_0} \\
\end{align}
$$
Generalizing this pattern to higher order systems
$$
\begin{align}
\sum_{k=0}^N a_k \frac{d^k y(t)}{dt^k} &= \sum_{k=0}^M b_k \frac{d^k x(t)}{dt^k} \\
\\
H(s) &= \frac{\sum_{k=0}^M b_k s^k}{\sum_{k=0}^N a_k s^k} \\
\end{align}
$$
Note that this result does not include specification for ROC. ROC is determined by stability or causality information that is provided with the problem.
First Order Systems
The generic first order lowpass system is represented by
$$
\begin{align}
\tau \frac{dy(t)}{dt} + y(t) &= b_0 x(t) \\
\end{align}
$$
where $\tau$ is the “time constant” of the system as we will see shortly. Taking the Laplace Transform, we have
$$
\begin{align}
\tau s Y(s) + Y(s) &= b_0 X(s) \\
Y(s) [\tau s + 1] &= b_0 X(s) \\
\frac{Y(s)}{X(s)} &= \frac{b_0}{\tau s + 1} \\
H(s) &= b_0 \frac{1}{\tau s + 1} \\
\end{align}
$$
Impulse and Step Response
Noticing that this result resembles the exponential decay transform, we can find the impulse response of the system.
$$
\begin{align}
e^{-at} u(t) &\stackrel{\mathscr{L}}{\leftrightarrow} \frac{1}{s + a} &&Re\{s\} > -Re\{a\} \\
\\
H(s) &= \frac{b_0}{\tau} \frac{1}{s + 1/\tau} &&Re\{s\} > -Re\{1/\tau\} \\
h(t) &= \frac{b_0}{\tau} e^{-t/\tau} u(t) &&Re\{s\} > -Re\{1/\tau\} \\
\end{align}
$$
The step response may be found directly by integrating the impulse response.
$$
\begin{align}
s(t) &= \int_{-\infty}^{t} h(x) dx \\
s(t) &= \frac{b_0}{\tau} \int_{-\infty}^{t} e^{-x/\tau} u(x) dx &&Re\{s\} > -Re\{1/\tau\} \\
s(t) &= \frac{b_0}{\tau} u(t) \int_{0}^{t} e^{-x/\tau} dx &&Re\{s\} > -Re\{1/\tau\} \\
s(t) &= \frac{b_0}{\tau} u(t) \left[ -\tau e^{-x/\tau} \right]_{x=0}^{t} &&Re\{s\} > -Re\{1/\tau\} \\
s(t) &= -b_0 u(t) \left[ e^{-x/\tau} \right]_{x=0}^{t} &&Re\{s\} > -Re\{1/\tau\} \\
s(t) &= -b_0 u(t) \left[ e^{-t/\tau} – 1\right] &&Re\{s\} > -Re\{1/\tau\} \\
s(t) &= b_0 \left[ 1 – e^{-t/\tau} \right] u(t) &&Re\{s\} > -Re\{1/\tau\} \\
\end{align}
$$
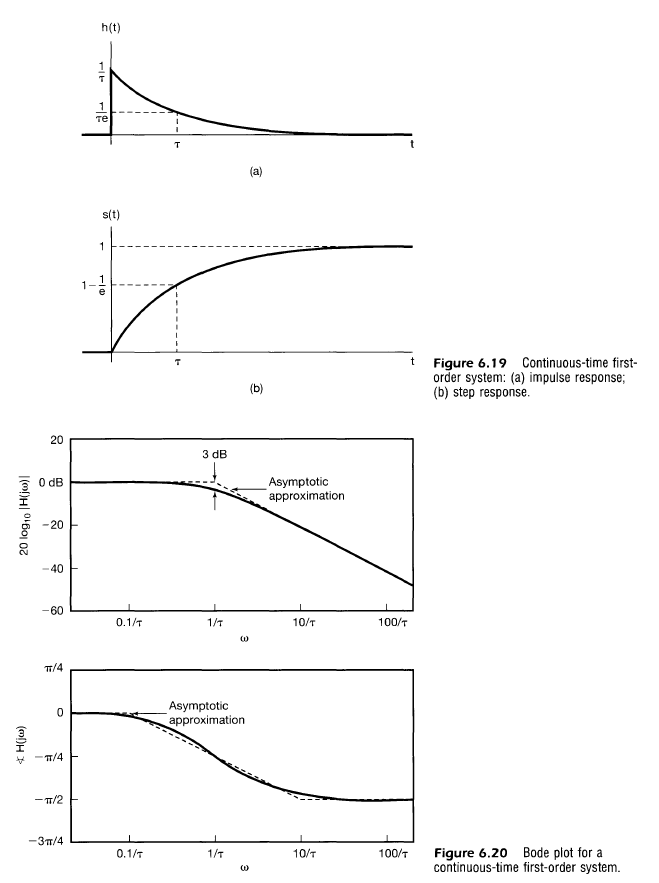
Note
- $t=\tau \rightarrow 37\%$ to final value
- $t=2\tau \rightarrow 13.5\%$ to final value
- $t=3\tau \rightarrow 5.00\%$ to final value
- No ringing
Rise Time
Time $t_1$ at which output reaches a known value, $y_1$ is determined from
$$
\begin{align}
y_1 &= b_0 \left[ 1 – e^{- t_1/\tau} \right] &&\tau > 0 &&t > 0 \\
\frac{y_1}{b_0} &= 1 – e^{- t_1/\tau} &&\tau > 0 &&t > 0 \\
e^{- t_1/\tau} &= 1 – \frac{y_1}{b_0} &&\tau > 0 &&t > 0 \\
– t_1/\tau &= \ln \left(1 – \frac{y_1}{b_0}\right) &&\tau > 0 &&t > 0 \\
t_1 &= – \tau \ln \left(1 – \frac{y_1}{b_0}\right) &&\tau > 0 &&t > 0 \\
t_1 &= – \tau \ln \left(\frac{b_0 – y_1}{b_0}\right) &&\tau > 0 &&t > 0 \\
t_1 &= \tau \ln \left(\frac{b_0}{b_0 – y_1}\right) &&\tau > 0 &&t > 0 \\
\end{align}
$$
This can be checked using $y_1 = 0.95 b_0$ in which case $t_1 \approx 3 \tau$ as expected.
Note that this equation assumes that input to system is unscaled unity step while system has gain of $b_0$. If input is scaled unity step, make sure $s(t)$ equation makes sense before substituting in $b_0$. In other words,
$$
\begin{align}
Y(j \omega) = b_0 \frac{1}{1 + j \omega \tau} U(j \omega) &\implies t_1 = \tau \ln \left(\frac{b_0}{b_0 – y_1}\right) &&\tau > 0 &&t > 0 \\
\\
Y(j \omega) = b_0 \frac{1}{1 + j \omega \tau} [C U(j \omega)] = [C b_0] \frac{1}{1 + j \omega \tau} U(j \omega) &\implies t_1 = \tau \ln \left(\frac{C b_0}{C b_0 – y_1}\right) &&\tau > 0 &&t > 0 \\
\end{align}
$$
Continuing on we can assume that rise time occurs relative to some percentage of the final output, $p$. In other words, the “clock” that measures rise time starts when the output is at $pb_0$ and ends when the output reaches $(1-p)b_0$.
$$
\begin{align}
t_1 &= \tau \ln \left( \frac{b_0}{b_0 – p b_0} \right) \\
t_1 &= \tau \ln \left( \frac{1}{1 – p} \right) \\
t_1 &= -\tau \ln(1-p) \\
\\
t_2 &= \tau \ln \left( \frac{b_0}{b_0 – (1-p) b_0} \right) \\
t_2 &= \tau \ln \left( \frac{1}{1 – (1-p)} \right) \\
t_2 &= \tau \ln \left( \frac{1}{p} \right) \\
t_2 &= -\tau \ln(p) \\
\\
t_r &= t_2 – t_1 \\
t_r &= (-\tau \ln(p)) – (-\tau \ln(1-p)) \\
t_r &= \tau [\ln(1-p) – \ln(p)] \\
t_r &= \tau \ln \left( \frac{1-p}{p} \right) \\
\end{align}
$$
So the rise time is only dependent on the chosen $p$ and system $\tau$, not the step size.
For 10% rise time, we have $t_r \approx 2.2 \tau$.
Settling Time
Similar to above, settling time is duration between step input and when output reaches percentage $p$ below final value.
$$
\begin{align}
t_s &= \tau \ln \left( \frac{b_0}{b_0 – (1-p) b_0} \right) \\
t_s &= \tau \ln \left( \frac{1}{1 – (1-p)} \right) \\
t_s &= \tau \ln \left( \frac{1}{p} \right) \\
t_s &= -\tau \ln(p) \\
\end{align}
$$
For 2% settling time, we have $t_s \approx 3.9 \tau$
Asymptote Approximations
Magnitude
$$
\begin{align}
20\log_{10} |H(j \omega)| &= 20\log_{10} \left| \frac{b_0}{1 + j \omega \tau} \right| &&\tau > 0 \\
20\log_{10} |H(j \omega)| &= 20\log_{10} b_0 – 20\log_{10} \left| 1 + j \omega \tau \right| &&\tau > 0 \\
20\log_{10} |H(j \omega)| &= 20\log_{10} b_0 – 20\log_{10} \sqrt{1^2 + (\omega \tau)^2 } &&\tau > 0 \\
20\log_{10} |H(j \omega)| &= 20\log_{10} b_0 – 10\log_{10} \left[ 1 + (\omega \tau)^2 \right] &&\tau > 0
\end{align}
$$
Asymptotes are generalized as
$$
20\log_{10} |H(j \omega)| \approx \cases{
\begin{align}
20\log_{10} b_0 &&\omega \leq \omega_n \\
20\log_{10} b_0 – 20\log_{10} \tau – 20\log_{10} \omega &&\omega \geq \omega_n \\
\end{align}
}
$$
where at frequencies beyond $\omega_n$, the output signal decays at -20 dB per decade.
$\omega_n$ can be found by finding the point at which these lines meet i.e. equating
$$
\begin{align}
20\log_{10} b_0 &= 20\log_{10} b_0 – 20\log_{10} \tau – 20\log_{10} \omega_n \\
0 &= \log_{10} \tau + \log_{10} \omega_n \\
0 &= \log_{10} \left( \tau \omega_n \right) \\
1 &= \tau \omega_n \\
\omega_n &= 1 / \tau \\
\end{align}
$$
So as $\tau$ gets larger, the cutoff point reduces in frequency.
Note also that the actual magnitude at $\omega_n$ is
$$
\begin{align}
20\log_{10} |H(j \omega_n)| &= 20\log_{10} \left| \frac{b_0}{1 + j} \right| &&\omega = \omega_n = 1/ \tau \\
20\log_{10} |H(j \omega_n)| &= 20\log_{10} \frac{b_0}{\sqrt{1^2 + 1^2}} &&\omega = \omega_n = 1/ \tau \\
20\log_{10} |H(j \omega_n)| &= 20\log_{10} \frac{b_0}{\sqrt{2}} &&\omega = \omega_n = 1/ \tau \\
20\log_{10} |H(j \omega_n)| &= 20\log_{10} b_0 – 20\log_{10} \sqrt{2} &&\omega = \omega_n = 1/ \tau \\
20\log_{10} |H(j \omega_n)| &= 20\log_{10} b_0 – 10\log_{10} 2 &&\omega = \omega_n = 1/ \tau \\
20\log_{10} |H(j \omega_n)| &\approx 20\log_{10} b_0 – 3.010 &&\omega = \omega_n = 1/ \tau \\
\end{align}
$$
which is why this point is also often called the -3 dB point. Note that this is the point where the output signal power is halved from the DC case.
$$
\begin{align}
20\log_{10} |H(j \omega_n)| &= 10\log_{10} \frac{b_0^2}{2} &&\omega = \omega_n = 1/ \tau \\
\end{align}
$$
Phase
$$
\begin{align}
\angle H(j\omega) &= \angle \left[ \frac{b_0}{1 + j \omega \tau} \right] \\
\angle H(j\omega) &= \angle b_0 – \angle \left[1 + j \omega \tau \right] \\
\angle H(j\omega) &= – \tan^{-1} (\omega \tau) && b_0 \in \mathbb{R}\\
\end{align}
$$
So in effect the phase plot looks like an inverse tangent plot flipped about the x axis. Notice also that if $\tau$ is large, it effectively squishes the curve in x so that lower frequency input signals are given more of a phase shift.
Asymptotic approximations are generally used on a graph where the x axis is $\log(\omega)$. This complicates matters somewhat, but helps if we define a new variable for the logarithmic x axis, $\omega_d$ where
$$
\begin{align}
\omega_d &= \log_{10}(\omega) \\
10^{\omega_d} &= \omega \\
\end{align}
$$
We would like asymptotes for when the $\tan^{-1}$ curve looks generally flat and around the inflection point. The flat sections are simpler to derive in that
$$
\angle H(j \omega) \approx \cases{
\begin{align}
0 &&\omega \leq \omega_{low} \\
\text{log(x) is linear} && \omega_{low} < \omega < \omega_{high} \\
\frac{\pi}{2} && \omega \geq \omega_{high}
\end{align}
}
$$
We now need to determine the slope of the linear region which will in turn determine $\omega_{low}$ and $\omega_{high}$.
Let’s now do some derivatives on the phase formula to look at possible asymptotes
$$
\angle H(j 10^{\omega_d}) = -\tan^{-1}(\tau 10^{\omega_d})
$$
First derivative:
$$
\begin{align}
\frac{d}{d \omega_d} \angle H(j 10^{\omega_d}) &= -\frac{1}{1 + (\tau 10^{\omega_d})^2} \cdot \tau 10^{\omega_d} \ln(10) \\
\frac{d}{d \omega_d} \angle H(j 10^{\omega_d}) &= -\ln(10) \frac{\tau 10^{\omega_d}}{1 + (\tau 10^{\omega_d})^2} \\
\end{align}
$$
Second derivative:
$$
\begin{align}
\frac{d^2}{d \omega_d^2} \angle H(j 10^{\omega_d}) &= -\ln(10) \frac{
[1 + (\tau 10^{\omega_d})^2] \tau 10^{\omega_d} \ln(10) – \tau 10^{\omega_d}[2 \tau 10^{\omega_d} \cdot \tau 10^{\omega_d} \ln(10)]}
{[1 + (\tau 10^{\omega_d})^2]^2} \\
\frac{d^2}{d \omega_d^2} \angle H(j 10^{\omega_d}) &= -\ln(10) \frac{
\tau 10^{\omega_d} \ln(10) + (\tau 10^{\omega_d})^3 \ln(10) – 2 (\tau 10^{\omega_d})^3 \ln(10)}
{[1 + (\tau 10^{\omega_d})^2]^2} \\
\frac{d^2}{d \omega_d^2} \angle H(j 10^{\omega_d}) &= -\ln(10) \frac{
\tau 10^{\omega_d} \ln(10) – (\tau 10^{\omega_d})^3 \ln(10)}
{[1 + (\tau 10^{\omega_d})^2]^2} \\
\frac{d^2}{d \omega_d^2} \angle H(j 10^{\omega_d}) &= -2 \ln(10) \frac{
\tau 10^{\omega_d} – (\tau 10^{\omega_d})^3}
{[1 + (\tau 10^{\omega_d})^2]^2} \\
\frac{d^2}{d \omega_d^2} \angle H(j 10^{\omega_d}) &= -2\ln(10) \tau 10^{\omega_d} \frac{
1 – (\tau 10^{\omega_d})^2}
{[1 + (\tau 10^{\omega_d})^2]^2} \\
\end{align}
$$
Inflection point when
$$
\begin{align}
1 – (\tau 10^{\omega_d})^2 = 0 \\
(\tau 10^{\omega_d})^2 = 1 \\
\tau 10^{\omega_d} = 1 \\
10^{\omega_d} = \frac{1}{\tau} \\
\omega = \frac{1}{\tau} \\
\end{align}
$$
Note also that when $\omega = 10^{\omega_d} = 1 / \tau$ we have
$$
\begin{align}
\left[ \frac{d}{d \omega_d} \angle H(j 10^{\omega_d}) \right]_{10^{\omega_d} = 1/\tau} &= -\ln(10) \frac{1}{1 + 1^2} \\
\left[ \frac{d}{d \omega_d} \angle H(j 10^{\omega_d}) \right]_{10^{\omega_d} = 1/\tau} &= – \frac{1}{2} \ln(10) \\
\left[ \frac{d}{d \omega_d} \angle H(j 10^{\omega_d}) \right]_{10^{\omega_d} = 1/\tau} &\approx -1.15 \\
\end{align}
$$
and
$$
\begin{align}
\left[ \angle H(j 10^{\omega_d}) \right]_{10^{\omega_d} = 1/\tau} &= -\tan^{-1}(1) \\
\left[ \angle H(j 10^{\omega_d}) \right]_{10^{\omega_d} = 1/\tau} &= -\frac{\pi}{4} \\
\end{align}
$$
So in summary the phase curve passes through the point $\omega = 1 / \tau, \angle H = -\pi/4$ with a decreasing slope, and there is an inflection point at this location when plotted on the log scale.
Using point-slope form, we can also derive an equation for this approximation line as
$$
\begin{align}
\angle H – \angle H_0 &\approx m (\omega_d – \omega_{0,d}) \\
\angle H &\approx m (\omega_d – \omega_{0,d}) + \angle H_0 \\
\angle H &\approx m [\omega_d – \log_{10} (1/\tau)] – \pi/4 \\
\angle H &\approx m [\log_{10} (\omega) – \log_{10} (1/\tau)] – \pi/4 \\
\angle H &\approx m [\log_{10} (\omega) + \log_{10} (\tau)] – \pi/4 \\
\angle H &\approx m \log_{10} (\omega \tau) – \pi/4 \\
\end{align}
$$
Now we can set $m$ to be the slope found earlier at the inflection point ($\approx -1.15$). However, as this an approximation generally used for drawing by hand, it is often more convenient to use the slope $- \pi / 4 \approx -0.785$. This gives us the approximation line at the inflection point as
$$
\begin{align}
\angle H \approx – \frac{\pi}{4} \log_{10} (\omega \tau) – \pi/4 \\
\angle H \approx – \frac{\pi}{4} \left[ \log_{10} (\omega \tau) + 1 \right] \\
\end{align}
$$
Note that this is easier to draw on the graph with the logarithmic x-axis because when $\omega = 1/\tau \cdot 10^{-1}$ (a decade lower in frequency) we get
$$
\begin{align}
\angle H \approx – \frac{\pi}{4} \left[ \log_{10} (10^{-1}) + 1 \right] \\
\angle H \approx 0 \\
\end{align}
$$
which is the first horizontal asymptote line and when $\omega = 1/\tau \cdot 10^{1}$ (a decade higher in frequency) we get
$$
\begin{align}
\angle H &\approx – \frac{\pi}{4} \left[ \log_{10} (10^{1}) + 1 \right] \\
\angle H &\approx – \frac{\pi}{4} \left[ 1 + 1 \right] \\
\angle H &\approx – \frac{\pi}{2} \\
\end{align}
$$
Putting everything together, we arrive at the asymptote summary
$$
\angle H(j \omega) \approx \cases{
\begin{align}
&0 &&\omega \leq \frac{10^{-1}}{\tau} \\
&- \frac{\pi}{4} \left[ \log_{10} (\omega \tau) + 1 \right] && \frac{10^{-1}}{\tau} < \omega < \frac{10^{1}}{\tau} \\
&\frac{\pi}{2} && \omega \geq \frac{10^{1}}{\tau}
\end{align}
}
$$
First Order Highpass Filter
We can use similar principles as above to define a highpass filter. Consider a filter described by
$$
\begin{align}
\tau \frac{d y(t)}{dt} + y(t) &= \tau \frac{d x(t)}{dt} \\
\\
H(s) &= \frac{\tau s}{\tau s + 1} \\
\end{align}
$$
The Fourier Transform is
$$
\begin{align}
H(j \omega) &= \frac{j \tau \omega}{j \tau \omega + 1} \\
\\
|H(j \omega)| &= \frac{\tau \omega}{\sqrt{(\tau \omega)^2 + 1} } \\
\end{align}
$$
Note that the frequency response resembles a high-pass filter.
$$
\begin{align}
\lim_{\omega \to 0} |H(j \omega)| &= \frac{0}{\sqrt{0 + 1} } \\
\lim_{\omega \to 0} |H(j \omega)| &= 0 \\
\\
\lim_{\omega \to \infty} |H(j \omega)| &= \frac{\tau}{\sqrt{\tau^2} } \\
\lim_{\omega \to \infty} |H(j \omega)| &= 1 \\
\end{align}
$$
The -3 dB Frequency is the same as in the lowpass case due to the denominator, $\omega_n = 1/\tau$
$$
\begin{align}
|H(j \omega_n)| &= \frac{\tau \omega_n}{\sqrt{(\tau \omega_n)^2 + 1} } \\
|H(j \omega_n)| &= \frac{1}{\sqrt{(1)^2 + 1} } \\
|H(j \omega_n)| &= \frac{1}{\sqrt{2} } \\
|H(j \omega_n)|^2 &= \frac{1}{2} \\
\end{align}
$$
Examples
Bathtub (Own Example)
Imagine a hose with water coming out at constant speed $u_{in}(t)$ with a cross-sectional flow area of $A_{in}$. If that water enters a tub, we would need initial conditions to determine the volume of water, $V_{tub}$ deposited in the tub. However, we can model the system as a differential equation and determine the rate at which the water volume in the tub increases, $\dot{V}_{tub}(t)$.
$$
\begin{align}
\dot{V}_{tub}(t) = A_{in} u_{in}(t)
\end{align}
$$
Now, if water is also exiting the tub through some hose of cross-sectional area $A_{out}$ and speed $u_{out}$ we can modify this equation.
$$
\begin{align}
\dot{V}_{tub}(t) = A_{in} u_{in}(t) – A_{out} u_{out}(t) \\
\end{align}
$$
Note that the above is essentially a mass balance equation. We can rewrite this equation with some additional assumptions:
- Tub of constant horizontal area $V_{tub}(t) = A_{tub} y_{tub}(t)$
- Flow rate out of tub is linear relationship determined by height of water, $u_{out}(t) = k \rho g y_{tub}(t) = C y_{tub}(t)$
$$
\begin{align}
\frac{d}{dt} V_{tub}(t) &= A_{in} u_{in}(t) – A_{out} u_{out}(t) \\
\frac{d}{dt} A_{tub} y_{tub}(t) &= A_{in} u_{in}(t) – C y_{tub}(t) \\
A_{tub} \frac{d}{dt} y_{tub}(t) + C y_{tub}(t) &= A_{in} u_{in}(t) \\
\end{align}
$$
Note that the above equation describes a first order system. Applying the Laplace transform, we can now determine the system response.
$$
\begin{align}
A_{tub} s Y_{tub}(s) + C Y_{tub}(s) &= A_{in} U_{in}(s) \\
Y_{tub}(s) [A_{tub} s + C] &= A_{in} U_{in}(s) \\
\frac{Y_{tub}(s)}{U_{in}(s)} &= \frac{A_{in}}{A_{tub} s + C} \\
H(s) &= \frac{A_{in}}{C} \frac{1}{(A_{tub}/C) s + 1} \\
\end{align}
$$
Rearranging into Tau Form, we find the following results
$$
\begin{align}
\tau &= \frac{A_{tub}}{C} \\
b_0 &= \frac{A_{in}}{C} \\
\\
h(t) &= \frac{A_{in}}{C} \frac{C}{A_{tub}} e^{-t/(A_{tub}/C)} u(t) \\
h(t) &= \frac{A_{in}}{A_{tub}} e^{-(C/A_{tub}) t} u(t) \\
\\
s(t) &= \frac{A_{in}}{C} \left[ 1 – e^{-(C/A_{tub}) t} \right] u(t) \\
\end{align}
$$
Note that for the step response
$$
\begin{align}
\lim_{t \to \infty} s(t) = \frac{A_{in}}{C} \\
\lim_{t \to \infty} s(t) = \frac{A_{in}}{k \rho g} \\
\end{align}
$$
which suggests the long term height of the water is determined solely by the input hose cross-section and chosen input flow rate (input to our system).
Also note that the time constant $\tau = A_{tub}/k \rho g$ matches our intuition in that increasing the tub cross-sectional area $A_{tub}$ increases the time constant and the height change is slower. More subtly, increasing the fluid density or gravity decreases the constant (output height is reached more quickly, but the output height in the long term is also lower as noted previously.
Above we made the assumption that the outgoing velocity was linearly related to the height of water in the tub.
$$
u_{out}(t) = C y_{tub}(t)
$$
If instead we use the Bernoulli relation across the tub drain such that
$$
\begin{align}
\rho g y_{tub}(t) &= \frac{1}{2} \rho u_{out}^2 \\
u_{out}^2 &= 2 g y_{tub}(t) \\
u_{out} &= \sqrt{2 g} \sqrt{y_{tub}(t)} \\
\end{align}
$$
we end up with a more complex differential equation which is not immediately solvable.
Second Order Systems
A second order system is a system where the Laplace transform has an $s^2$ term i.e. a second derivative exists in the system model equation. In general we will be concerned with stable systems, and to achieve this the order of the denominator must be greater than or equal to the numerator, so we focus on cases when the $s^2$ term is in the denominator.
Second Order Transforms
A generic second order system that is a good starting point for analysis is the second-order lowpass filter that uses the following common terms below. For the remaining analyses we will assume a lowpass filter unless otherwise stated.
$$
\begin{align}
\frac{d^2 y(t)}{dt^2} + 2 \zeta \omega_n \frac{d y(t)}{dt} + \omega_n^2 y(t) = b_0 \omega_n^2 x(t) \\
\end{align}
$$
Second Order System Laplace Transform
$$
\begin{align}
H(s) &= b_0 \frac{\omega_n^2}{s^2 + 2 \zeta \omega_n s + \omega_n^2} \\
\end{align}
$$
To get an idea of where the poles are, we can simply employ the quadratic equation for the denominator.
$$
\begin{align}
s_p &= \frac{-2 \zeta \omega_n \pm \sqrt{(2 \zeta \omega_n)^2 – 4 \omega_n^2}}{2} \\
s_p &= -\zeta \omega_n \pm \frac{1}{2} \sqrt{4 \zeta^2 \omega_n^2 – 4 \omega_n^2} \\
s_p &= -\zeta \omega_n \pm \frac{1}{2} \sqrt{4 \omega_n^2( \zeta^2 – 1)} \\
s_p &= -\zeta \omega_n \pm \omega_n \sqrt{ \zeta^2 – 1} \\
\end{align}
$$
The poles may then be described as
$$
\begin{align}
c_1 &= -\zeta \omega_n + \omega_n \sqrt{\zeta^2-1} \\
c_2 &= -\zeta \omega_n – \omega_n \sqrt{\zeta^2-1} \\
\end{align}
$$
And the system equation may be rewritten in terms of the poles which is easier for partial fraction expansion.
$$
\begin{align}
H(s) &= b_0 \frac{\omega_n^2}{(s – c_1)(s – c_2)} \\
\end{align}
$$
A minor variation of this system equation is sometimes encountered that uses the Quality Factor, $Q$.
$$
\begin{align}
Q &= \frac{1}{2 \zeta} \\
2 \zeta &= \frac{1}{Q}
\\
H(s) &= b_0 \frac{\omega_n^2}{s^2 + \frac{\omega_n}{Q} s + \omega_n^2} \\
\end{align}
$$
To determine stability, we can look at
$$
Re\{c_{1,2}\} = -\zeta \omega_n
$$
In other words, assuming that $\omega_n > 0$, a negative $\zeta$ indicates an unstable system, and a positive $\zeta$ indicates a stable one.
Second Order System Fourier Transform
$$
\begin{align}
H(j \omega) &= b_0 \frac{\omega_n^2}{(j \omega)^2 + 2 \zeta \omega_n (j \omega) + \omega_n^2} \\
H(j \omega) &= b_0 \frac{\omega_n^2}{-\omega^2 + j 2 \zeta \omega_n \omega + \omega_n^2} \\
H(j \omega) &= b_0 \frac{\omega_n^2}{[\omega_n^2-\omega^2] + j 2 \zeta \omega_n \omega} \\
H(j \omega) &= b_0 \frac{1}{[1-(\omega/\omega_n)^2] + j 2 \zeta (\omega/\omega_n)} \\
\end{align}
$$
From the last equation, we can see that changing $\omega_n$ is equivalent to scaling the system response in the frequency domain.
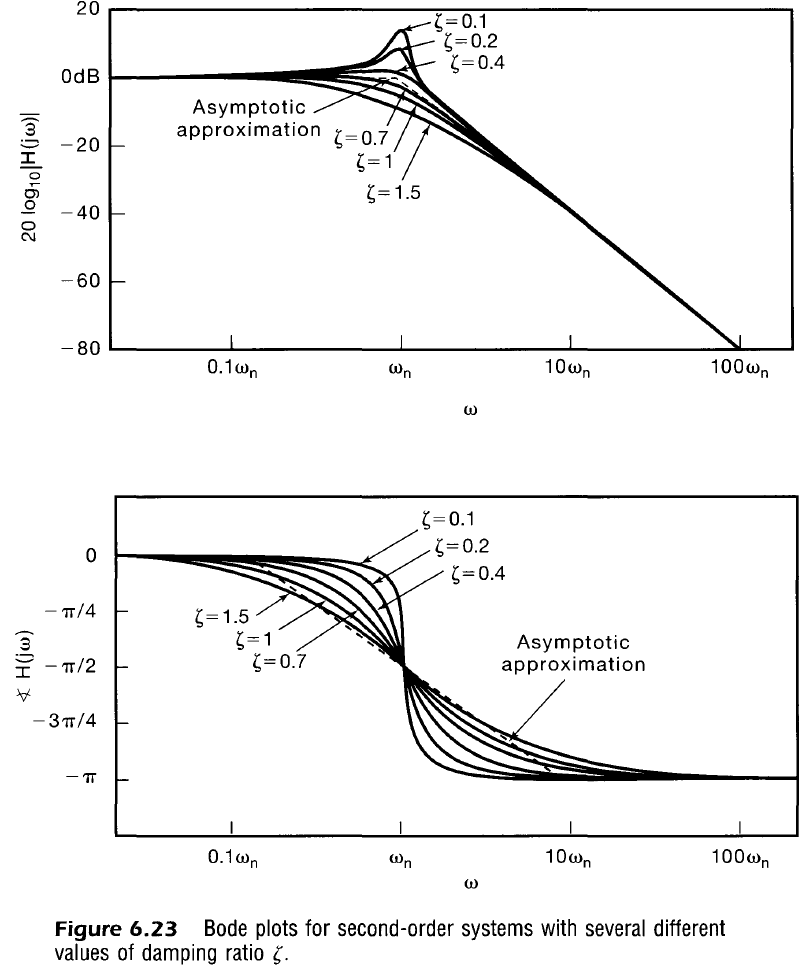
Second Order System Magnitude
$$
\begin{align}
|H(j \omega)| &= \left| b_0 \frac{\omega_n^2}{(j \omega)^2 + 2 \zeta \omega_n (j \omega) + \omega_n^2} \right| \\
|H(j \omega)| &= b_0 \frac{\omega_n^2}{\left| (j \omega)^2 + 2 \zeta \omega_n (j \omega) + \omega_n^2 \right|} \\
|H(j \omega)| &= b_0 \frac{\omega_n^2}{\left| (\omega_n^2 – \omega^2) + j (2 \zeta \omega_n \omega) \right|} \\
|H(j \omega)| &= b_0 \frac{\omega_n^2}{\sqrt{(\omega_n^2 – \omega^2)^2 + (2 \zeta \omega_n \omega)^2}} \\
|H(j \omega)| &= b_0 \frac{\omega_n^2}{\sqrt{\omega_n^4 – 2 \omega^2 \omega_n^2 + \omega^4 + 4 \zeta^2 \omega^2 \omega_n^2}} \\
|H(j \omega)| &= b_0 \frac{\omega_n^2}{\sqrt{\omega_n^4 + \omega^4 + 2 \omega^2 \omega_n^2(2 \zeta^2 – 1)}} \\
\end{align}
$$
Or solving in a different manner
$$
\begin{align}
|H(j \omega)| &= \frac{\omega_n^2}{|j \omega – c_1||j \omega – c_2|} \\
|H(j \omega)| &= \frac{\omega_n^2}{\sqrt{(\omega^2 + c_1^2)(\omega^2 + c_2^2)}} \\
|H(j \omega)| &= \frac{\omega_n^2}{\sqrt{\omega^4 + \omega^2 (c_1^2 + c_2^2) + (c_1 c_2)^2}} \\
\end{align}
$$
Note that
$$
\begin{align}
c_1^2 &= (\zeta \omega_n)^2 – 2 \zeta \omega_n^2 \sqrt{\zeta^2-1} + \omega_n^2(\zeta^2-1) \\
c_1^2 &= \omega_n^2 (\zeta^2 – 2 \zeta \sqrt{\zeta^2-1} + \zeta^2-1) \\
c_1^2 &= \omega_n^2 (2\zeta^2 – 2 \zeta \sqrt{\zeta^2-1} – 1) \\
c_1^2 &= \omega_n^2 [(2\zeta^2 – 1) – 2 \zeta \sqrt{\zeta^2-1}] \\
\\
c_2^2 &= (\zeta \omega_n)^2 + 2 \zeta \omega_n^2 \sqrt{\zeta^2-1} + \omega_n^2(\zeta^2-1) \\
c_2^2 &= \omega_n^2 (\zeta^2 + 2 \zeta \sqrt{\zeta^2-1} + \zeta^2-1) \\
c_2^2 &= \omega_n^2 (2\zeta^2 + 2 \zeta \sqrt{\zeta^2-1} – 1) \\
c_2^2 &= \omega_n^2 [(2\zeta^2 – 1) + 2 \zeta \sqrt{\zeta^2-1}] \\
\\
c_1^2 + c_2^2 &= \omega_n^2 [(2\zeta^2 – 1) – 2 \zeta \sqrt{\zeta^2-1} + (2\zeta^2 – 1) + 2 \zeta \sqrt{\zeta^2-1}] \\
c_1^2 + c_2^2 &= 2 \omega_n^2 (2\zeta^2 – 1) \\
\\
c_1^2 c_2^2 &= \omega_n^4 [(2\zeta^2 – 1) – 2 \zeta \sqrt{\zeta^2-1}][(2\zeta^2 – 1) + 2 \zeta \sqrt{\zeta^2-1}] \\
c_1^2 c_2^2 &= \omega_n^4 [(2\zeta^2 – 1)^2 – 4 \zeta^2 (\zeta^2-1)] \\
c_1^2 c_2^2 &= \omega_n^4 [4 \zeta^4 – 4 \zeta^2 + 1 – 4 \zeta^4 + 4 \zeta^2] \\
c_1^2 c_2^2 &= \omega_n^4 \\
\end{align}
$$
So
$$
\begin{align}
|H(j \omega)| &= \frac{\omega_n^2}{\sqrt{\omega^4 + \omega^2 [2 \omega_n^2 (2\zeta^2 – 1)] + \omega_n^4}} \\
|H(j \omega)| &= \frac{\omega_n^2}{\sqrt{\omega_n^4 + \omega^4 + 2 \omega^2 \omega_n^2 (2\zeta^2 – 1)}} \\
\end{align}
$$
which is the same as above.
Second Order System Magnitude Asymptotes
$$
\begin{align}
20 \log_{10} |H(j \omega)| &= 20 \log_{10} \left| b_0 \frac{1}{[1-(\omega/\omega_n)^2] + j 2 \zeta (\omega/\omega_n)} \right| \\
20 \log_{10} |H(j \omega)| &= 20 \log_{10} | b_0 | – 20 \log_{10} \left| [1-(\omega/\omega_n)^2] + j 2 \zeta (\omega/\omega_n) \right| \\
20 \log_{10} |H(j \omega)| &= 20 \log_{10} b_0 – 20 \log_{10} \left\{ \left[1 – (\omega/\omega_n)^2 \right]^2 + \left[ 2 \zeta (\omega / \omega_n) \right]^2 \right\}^{\frac{1}{2}} \\
20 \log_{10} |H(j \omega)| &= 20 \log_{10} b_0 – 10 \log_{10} \left\{ \left[1 – (\omega/\omega_n)^2 \right]^2 + \left[ 2 \zeta (\omega / \omega_n) \right]^2 \right\} \\
20 \log_{10} |H(j \omega)| &= 20 \log_{10} b_0 – 10 \log_{10} \left\{ \left[1 – (\omega/\omega_n)^2 \right]^2 + 4 \zeta^2 (\omega / \omega_n)^2 \right\} \\
\end{align}
$$
For small values of $\omega$, the magnitude plot can be assumed to be a constant. With some manipulation
$$
\begin{align}
20 \log_{10} |H(j \omega)| &= 20 \log_{10} b_0 – 10 \log_{10} \left\{ \left[\frac{\omega_n^2 – \omega^2}{\omega_n^2} \right]^2 + \frac{ 4 \zeta^2 \omega^2}{ \omega_n^2} \right\} \\
20 \log_{10} |H(j \omega)| &= 20 \log_{10} b_0 – 10 \log_{10} \left\{ \frac{ (\omega_n^2 – \omega^2)^2 + 4 \zeta^2 \omega^2 \omega_n^2}{\omega_n^4} \right\} \\
20 \log_{10} |H(j \omega)| &= 20 \log_{10} b_0 – 10 \log_{10} \left\{ (\omega_n^2 – \omega^2)^2 + 4 \zeta^2 \omega^2 \omega_n^2 \right\} + 40 \log_{10}(\omega_n)\\
20 \log_{10} |H(j \omega)| &= 20 \log_{10} b_0 – 10 \log_{10} \left\{ \omega_n^4 – 2 \omega^2 \omega_n^2 + \omega^4 + 4 \zeta^2 \omega^2 \omega_n^2 \right\} + 40 \log_{10}(\omega_n)\\
\end{align}
$$
we can see that the $\omega^4$ will dominate the middle term at increasing frequencies. In summary, the asymptotes become
$$
20 \log_{10} |H(j \omega)| \approx \cases{
\begin{align}
&20 \log_{10} b_0 &&\omega < \omega_n \\
&20 \log_{10} b_0 + 40 \log_{10} \omega_n – 40 \log_{10} \omega && \omega \geq \omega_n
\end{align}
}
$$
It is easy to verify that these two lines intersect when $\omega = \omega_n$. Note that after $\omega = \omega_n$ the magnitude plot is summarized by a downward sloping line at 40 dB per decade
Second Order System Angle
$$
\begin{align}
\angle H(j \omega) &= \angle \left[ b_0 \frac{1}{[1-(\omega/\omega_n)^2] + j 2 \zeta (\omega/\omega_n)} \right] \\
\angle H(j \omega) &= \angle b_0 – \angle \left[ 1-(\omega/\omega_n)^2 + j 2 \zeta (\omega/\omega_n) \right] \\
\angle H(j \omega) &= – \angle \left[ 1-(\omega/\omega_n)^2 + j 2 \zeta (\omega/\omega_n) \right] && b_0 \in \mathbb{R} \\
\angle H(j \omega) &= – \tan^{-1} \left[ \frac{2 \zeta (\omega / \omega_n )}{1 – (\omega / \omega_n)^2} \right] && b_0 \in \mathbb{R} \\
\end{align}
$$
Second Order System Angle Asymptotes
What makes defining asymptotes on a Bode plot difficult is the logarithmic frequency axis, but linear angle axis. To accommodate this, we can use the substitution for a new horizontal variable $\omega_d = \log_{10} \omega \implies \omega = 10^{\omega_d}$.
$$
\begin{align}
\angle H(j 10^{\omega_d}) &= – \tan^{-1} \left[ \frac{2 \zeta (10^{\omega_d} / \omega_n )}{1 – (10^{\omega_d} / \omega_n)^2} \right] && b_0 \in \mathbb{R} \\
\end{align}
$$
The calculus to solve for slope and inflection point here gets a bit harder, but we can assume we want to go with a similar asymptote approximation as before.
For low values of $\omega$, the the fraction has a small positive numerator and denominator near positive $1$, so $\angle H(j \omega) \approx -\tan^{-1}(0^+) = 0$
For high values of $\omega$ the fraction is dominated by the large negative number in the denominator, so this asymptote can be summarized by $\angle H(j \omega) \approx – \lim_{x \to \infty} \tan^{-1}(x/-x^2) = – \pi$. Note that if the negative sign is moved to the numerator, we get a slightly different answer depending on the range chosen for $\tan^{-1}$ ($[-\pi/2, \pi/2]$ or $[0,\pi]$).
The crossover point where $\angle H(j \omega) = – \pi/2$ is when the fraction becomes
$$
\begin{align}
-\frac{\pi}{2} &= – \tan^{-1} \left[ \frac{2 \zeta (\omega / \omega_n )}{1 – (\omega / \omega_n)^2} \right] \\
\tan \frac{\pi}{2} &= \frac{2 \zeta (\omega / \omega_n )}{1 – (\omega / \omega_n)^2} \\
\infty &= \frac{2 \zeta (\omega / \omega_n )}{1 – (\omega / \omega_n)^2} \\
1 – (\omega / \omega_n)^2 &= 0 \\
\omega/\omega_n &= 1 \\
\omega &= \omega_n \\
\end{align}
$$
Avoiding all the calculus needed to do a precise look at slope and inflection point at this location, we commonly handwave this region as being linear (on logarithmic frequency axis) between one decade before and after $\omega_n$. To summarize
$$
\angle H(j \omega) \approx \cases{
\begin{align}
&0 && \omega \leq \omega_n \cdot 10^{-1} \\
&-\frac{\pi}{2} \left[ \log_{10}{(\omega/\omega_n)} + 1\right] && \omega_n \cdot 10^{-1} < \omega < \omega_n \cdot 10^{1} \\
&-\pi && \omega \geq \omega_n \cdot 10^{1}
\end{align}
}
$$
This approximation does not depend on $\zeta$ which hinders how realistic the approximation is.
Overdamped Second Order Systems, $\zeta > 1$
Conducting partial fraction expansion we have
$$
\begin{align}
H(j \omega) &= b_0 \frac{\omega_n^2}{(j \omega – c_1)(j \omega – c_2)} \\
H(j \omega) &= b_0 \left[ \frac{A}{j \omega – c_1} + \frac{B}{j \omega – c_2} \right] \\
\\
b_0 A &= \left[ (j \omega – c_1) H(j \omega) \right]_{j \omega=c_1} \\
A &= \frac{\omega_n^2}{c_1 – c_2} \\
\\
b_0 B &= \left[ (j \omega – c_2) H(j \omega) \right]_{j \omega=c_2} \\
B &= \frac{\omega_n^2}{c_2 – c_1} \\
\end{align}
$$
Solving for $A$
$$
\begin{align}
A &= \frac{\omega_n^2}{c_1 – c_2} \\
A &= \frac{\omega_n^2}{2 \omega_n \sqrt{\zeta^2 – 1}} \\
A &= \frac{\omega_n}{2 \sqrt{\zeta^2 – 1}} \\
\end{align}
$$
Note that $B = -A$ so we can simplify the expansion with a new variable, $M$
$$
M = A = -B = \frac{\omega_n}{2 \sqrt{\zeta^2 – 1}}
$$
Partial fraction expansion then resembles
$$
\begin{align}
H(j \omega) &= b_0 \left[ \frac{M}{j \omega – c_1} – \frac{M}{j \omega – c_2} \right] \\
H(j \omega) &= b_0 M \left[ \frac{1}{j \omega – c_1} – \frac{1}{j \omega – c_2} \right] \\
H(j \omega) &= \frac{b_0 \omega_n}{2 \sqrt{\zeta^2 – 1}} \left[ \frac{1}{j \omega – c_1} – \frac{1}{j \omega – c_2} \right] \\
\end{align}
$$
Overdamped Second Order System Impulse Response, $\zeta > 1$
Recalling the transform of an exponential decay signal we may note that the expanded frequency response is a sum of two first order fractions to determine the impulse response.
$$
\begin{align}
e^{-at} u(t) &\stackrel{\mathcal{F}}{\leftrightarrow} \frac{1}{j \omega + a} \\
\\
h(t) &= b_0 M \left[ e^{c_1 t} – e^{c_2 t} \right] u(t) \\
h(t) &= \frac{b_0 \omega_n}{2 \sqrt{\zeta^2 – 1}} \left[ e^{-\zeta \omega_n t} e^{(\omega_n \sqrt{\zeta^2-1}) t} – e^{-\zeta \omega_n t} e^{-(\omega_n \sqrt{\zeta^2-1}) t } \right] u(t) \\
h(t) &= \frac{b_0 \omega_n}{2 \sqrt{\zeta^2 – 1}} e^{-\zeta \omega_n t} \left[ e^{(\omega_n \sqrt{\zeta^2-1}) t} – e^{-(\omega_n \sqrt{\zeta^2-1}) t} \right] u(t) \\
\end{align}
$$
Overamped Second Order System Step Response, $\zeta > 1$
Reference Nise Control Systems Section 4.5
$$
\begin{align}
s(t) &= \int_{-\infty}^{t} h(x) dx \\
s(t) &= \int_{-\infty}^{t} b_0 M \left[ e^{c_1 x} – e^{c_2 x} \right] u(x) dx \\
s(t) &= b_0 M u(t) \int_{0}^{t} \left[ e^{c_1 x} – e^{c_2 x} \right] dx \\
s(t) &= b_0 M u(t) \left\{ \int_{0}^{t} e^{c_1 x} dx – \int_{0}^{t} e^{c_2 x} dx \right\} \\
s(t) &= b_0 M u(t) \left\{ \left[ \frac{e^{c_1 x}}{c_1} \right]_{x=0}^{t} – \left[ \frac{e^{c_2 x}}{c_2} \right]_{x=0}^{t} \right\} \\
s(t) &= b_0 M u(t) \left\{ \left[ \frac{e^{c_1 t}}{c_1} – \frac{1}{c_1} \right] – \left[ \frac{e^{c_2 t}}{c_2} – \frac{1}{c_2} \right] \right\} \\
s(t) &= b_0 M u(t) \left\{ \frac{e^{c_1 t}}{c_1} – \frac{e^{c_2 t}}{c_2} + \frac{1}{c_2} – \frac{1}{c_1} \right\} \\
s(t) &= b_0 M u(t) \left\{ \frac{e^{c_1 t}}{c_1} – \frac{e^{c_2 t}}{c_2} + \frac{c_1 – c_2}{c_1 c_2} \right\} \\
\end{align}
$$
Note that
$$
\begin{align}
\frac{c_1 c_2}{c_1 – c_2} &= \frac
{(-\zeta \omega_n + \omega_n \sqrt{\zeta^2-1})(-\zeta \omega_n – \omega_n \sqrt{\zeta^2-1})}
{-\zeta \omega_n + \omega_n \sqrt{\zeta^2-1} – [-\zeta \omega_n – \omega_n \sqrt{\zeta^2-1}]} \\
\frac{c_1 c_2}{c_1 – c_2} &= \frac{\zeta^2 \omega_n^2 – \omega_n^2 (\zeta^2-1)}{2 \omega_n \sqrt{\zeta^2-1}} \\
\frac{c_1 c_2}{c_1 – c_2} &= \frac{\zeta^2 \omega_n^2 – \omega_n^2 \zeta^2 + \omega_n^2}{2 \omega_n \sqrt{\zeta^2-1}} \\
\frac{c_1 c_2}{c_1 – c_2} &= \frac{\omega_n^2}{2 \omega_n \sqrt{\zeta^2-1}} \\
\frac{c_1 c_2}{c_1 – c_2} &= \frac{\omega_n}{2 \sqrt{\zeta^2-1}} \\
\frac{c_1 c_2}{c_1 – c_2} &= M \\
\end{align}
$$
So we can simplify the equation above as
$$
\begin{align}
s(t) &= b_0 M u(t) \left\{ \frac{e^{c_1 t}}{c_1} – \frac{e^{c_2 t}}{c_2} + \frac{1}{M} \right\} \\
s(t) &= b_0 u(t) \left\{ M\left[ \frac{e^{c_1 t}}{c_1} – \frac{e^{c_2 t}}{c_2} \right] + 1 \right\} \\
s(t) &= b_0 u(t) \left\{ M\left[ \frac{c_2 e^{c_1 t} – c_1 e^{c_2 t}}{c_1 c_2} \right] + 1 \right\} \\
\end{align}
$$
If we instead wanted to use the general second order variables, we can substitute into this equation.
$$
\begin{align}
s(t) &= b_0 u(t) \left\{ \frac{\omega_n}{2 \sqrt{\zeta^2 – 1}} \left[ \frac{(-\zeta \omega_n – \omega_n \sqrt{\zeta^2 – 1}) e^{(-\zeta \omega_n + \omega_n \sqrt{\zeta^2 – 1}) t} – (-\zeta \omega_n + \omega_n \sqrt{\zeta^2 – 1}) e^{(-\zeta \omega_n – \omega_n \sqrt{\zeta^2 – 1}) t}}{(\zeta \omega_n)^2 – \omega_n^2(\zeta^2 – 1)} \right] + 1 \right\} \\
s(t) &= b_0 u(t) \left\{ \frac{\omega_n e^{-\zeta \omega_n t} }{2 \sqrt{\zeta^2 – 1}} \left[ \frac{(-\zeta \omega_n – \omega_n \sqrt{\zeta^2 – 1}) e^{\omega_n \sqrt{\zeta^2 – 1} t} – (-\zeta \omega_n + \omega_n \sqrt{\zeta^2 – 1}) e^{- \omega_n \sqrt{\zeta^2 – 1} t}}{\omega_n^2} \right] + 1 \right\} \\
s(t) &= b_0 u(t) \left\{ \frac{e^{-\zeta \omega_n t} }{2 \sqrt{\zeta^2 – 1}} \left[ \frac{-\zeta \omega_n e^{\omega_n \sqrt{\zeta^2 – 1} t} – \omega_n \sqrt{\zeta^2 – 1} e^{\omega_n \sqrt{\zeta^2 – 1} t} + \zeta \omega_n e^{- \omega_n \sqrt{\zeta^2 – 1} t} – \omega_n \sqrt{\zeta^2 – 1} e^{- \omega_n \sqrt{\zeta^2 – 1} t}}{\omega_n} \right] + 1 \right\} \\
s(t) &= b_0 u(t) \left\{ \frac{e^{-\zeta \omega_n t} }{2 \sqrt{\zeta^2 – 1}} \left[ -\zeta e^{\omega_n \sqrt{\zeta^2 – 1} t} – \sqrt{\zeta^2 – 1} e^{\omega_n \sqrt{\zeta^2 – 1} t} + \zeta e^{- \omega_n \sqrt{\zeta^2 – 1} t} – \sqrt{\zeta^2 – 1} e^{- \omega_n \sqrt{\zeta^2 – 1} t} \right] + 1 \right\} \\
s(t) &= b_0 u(t) \left\{ \frac{e^{-\zeta \omega_n t} }{2 \sqrt{\zeta^2 – 1}} \left[ – \sqrt{\zeta^2 – 1} \left( e^{ \omega_n \sqrt{\zeta^2 – 1} t} + e^{- \omega_n \sqrt{\zeta^2 – 1} t} \right) -\zeta \left( e^{\omega_n \sqrt{\zeta^2 – 1} t} – e^{-\omega_n \sqrt{\zeta^2 – 1} t} \right) \right] + 1 \right\} \\
s(t) &= b_0 u(t) \left\{ -\frac{e^{-\zeta \omega_n t}}{2} \left( e^{ \omega_n \sqrt{\zeta^2 – 1} t} + e^{- \omega_n \sqrt{\zeta^2 – 1} t} \right) -\frac{ \zeta e^{-\zeta \omega_n t} }{2 \sqrt{\zeta^2 – 1}} \left( e^{\omega_n \sqrt{\zeta^2 – 1} t} – e^{-\omega_n \sqrt{\zeta^2 – 1} t} \right) + 1 \right\} \\
\end{align}
$$
Underdamped Second Order Systems, $0 < \zeta < 1$
In general, most of the analysis mirrors the overdamped case. However, using $\zeta < 1$ introduces imaginary components of exponents which introduces some special phenomena of note.
Underdamped Second Order System Impulse Response
Recall from the overdamped impulse response that
$$
\begin{align}
h(t) &= \frac{b_0 \omega_n}{2 \sqrt{\zeta^2 – 1}} e^{-\zeta \omega_n t} \left[ e^{(\omega_n \sqrt{\zeta^2-1}) t} – e^{-(\omega_n \sqrt{\zeta^2-1}) t} \right] u(t) \\
\end{align}
$$
In the underdamped case, $0 < \zeta < 1$ and the exponent in the brackets has an imaginary component. In this case, it is simpler to express the exponent using
$$
\begin{align}
&\sqrt{\zeta^2 – 1} \\
&\sqrt{-1(1 – \zeta^2)} \\
&j \sqrt{1 – \zeta^2} \\
\end{align}
$$
which leaves our impulse response as
$$
\begin{align}
h(t) &= \frac{b_0 \omega_n}{2 j \sqrt{1-\zeta^2}} e^{-\zeta \omega_n t} \left[ e^{j (\omega_n \sqrt{1-\zeta^2})t} – e^{-j (\omega_n \sqrt{1-\zeta^2}) t} \right] u(t) \\
h(t) &= \frac{b_0 \omega_n}{\sqrt{1-\zeta^2}} e^{-\zeta \omega_n t} \sin \left[ \left(\omega_n \sqrt{1-\zeta^2} \right) t \right]
\end{align}
$$
which is effectively damped oscillatory behavior.
Underdamped Second Order System Step Response
Similarly to the impulse response, we can modify the overdamped step response for when $\zeta < 1$. We start with the general case
$$
\begin{align}
s(t) &= b_0 u(t) \left\{ -\frac{e^{-\zeta \omega_n t}}{2} \left( e^{ \omega_n \sqrt{\zeta^2 – 1} t} + e^{- \omega_n \sqrt{\zeta^2 – 1} t} \right) -\frac{ \zeta e^{-\zeta \omega_n t} }{2 \sqrt{\zeta^2 – 1}} \left( e^{\omega_n \sqrt{\zeta^2 – 1} t} – e^{-\omega_n \sqrt{\zeta^2 – 1} t} \right) + 1 \right\} \\
\end{align}
$$
and then substitute
$$
\begin{align}
\sqrt{\zeta^2 – 1} &= j \sqrt{1 – \zeta^2} &&\zeta < 1 \\
\end{align}
$$
to rewrite the step response as
$$
\begin{align}
s(t) &= b_0 u(t) \left\{ -\frac{e^{-\zeta \omega_n t}}{2} \left( e^{ j \omega_n \sqrt{1 – \zeta^2} t} + e^{- j\omega_n \sqrt{1 – \zeta^2} t} \right) -\frac{ \zeta e^{-\zeta \omega_n t} }{j2 \sqrt{1 – \zeta^2}} \left( e^{j \omega_n \sqrt{1 – \zeta^2} t} – e^{-j \omega_n \sqrt{1 – \zeta^2} t} \right) + 1 \right\} \\
s(t) &= b_0 u(t) \left\{ -e^{-\zeta \omega_n t}\cos( \omega_n \sqrt{1 – \zeta^2} t) -\frac{ \zeta e^{-\zeta \omega_n t}}{\sqrt{1 – \zeta^2}} \sin( \omega_n \sqrt{1 – \zeta^2} t) + 1 \right\} \\
s(t) &= b_0 u(t) \left\{1 – e^{-\zeta\omega_n t} \left[ \cos(\omega_n \sqrt{1 – \zeta^2}t) + \frac{\zeta}{\sqrt{1-\zeta^2}} \sin(\omega_n \sqrt{1-\zeta^2}t) \right] \right\} \\
\end{align}
$$
From linear combination identity, this may be rewritten as
$$
\begin{align}
a \cos(x) + b \sin(x) &= \text{sgn}(a) \sqrt{a^2 + b^2} \cos\left[x + \tan^{-1}\left(- \frac{b}{a}\right) \right] \\
\end{align}
$$
$$
\begin{align}
s(t) &= b_0 u(t) \left\{1 – e^{-\zeta\omega_n t} \sqrt{1 + \left(\frac{\zeta}{\sqrt{1 – \zeta^2}}\right)^2} \cos\left[ \omega_n\sqrt{1-\zeta^2}t + \tan^{-1}\left(-\frac{\frac{\zeta}{\sqrt{1 – \zeta^2}}}{1}\right) \right] \right\} \\
s(t) &= b_0 u(t) \left\{1 – e^{-\zeta\omega_n t} \sqrt{1 + \frac{\zeta^2}{1 – \zeta^2}} \cos\left[ \omega_n\sqrt{1-\zeta^2}t + \tan^{-1}\left(-\frac{\zeta}{\sqrt{1 – \zeta^2}}\right) \right] \right\} \\
s(t) &= b_0 u(t) \left\{1 – e^{-\zeta\omega_n t} \sqrt{\frac{(1 – \zeta^2) + \zeta^2}{1 – \zeta^2}} \cos\left[ \omega_n\sqrt{1-\zeta^2}t – \tan^{-1}\left(\frac{\zeta}{\sqrt{1 – \zeta^2}}\right) \right] \right\} \\
s(t) &= b_0 u(t) \left\{1 – e^{-\zeta\omega_n t} \sqrt{\frac{1}{1 – \zeta^2}} \cos\left[ \omega_n\sqrt{1-\zeta^2}t – \tan^{-1}\left(\frac{\zeta}{\sqrt{1 – \zeta^2}}\right) \right] \right\} \\
\end{align}
$$
which may be more helpful as the sinusoid terms have been reduced to one.
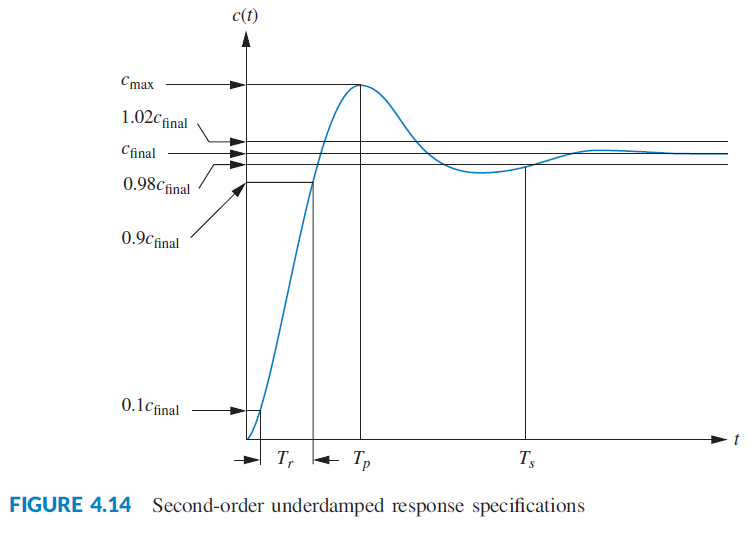
When input is a unit step to underdamped lowpass system, response signal can be described with
$$
S(s) = \frac{1}{s} \frac{\omega_n^2}{s^2 + 2 \zeta \omega_n s + \omega_n^2}
$$
Origin of Terms
Reference: Nise Control Systems Engineering
$\omega_n$ = undamped natural frequency. System oscillation frequency if no damping
$\zeta$ = damping ratio. Can be conceptualized as
$$
\begin{align}
\zeta = \frac{\text{Exponential decay frequency}}{\text{Natural Frequency}} \\
\zeta = \frac{1}{2\pi} \frac{\text{Natural Period}}{\text{Exponential time constant}} \\
\end{align}
$$
Note that this means damping has same characteristics relative to natural frequency i.e. time scale does not determine characteristics.
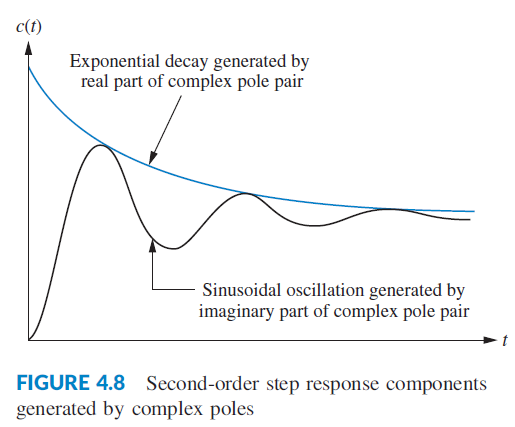
Consider a rational function with second order denominator.
$$
G(s) = \frac{b}{s^2 + as + b}
$$
If $a=0$, then we get
$$
G_{a=0}(s) = \frac{b}{s^2 + b}
$$
which we previously found to be a pure undamped oscillation with poles on $j \omega$ axis at $\pm j\sqrt{b}$. To put this in a more familiar form for undamped oscillation, we make the substitution
$$
\begin{align}
b = \omega_n^2 \\
\\
G_{a=0}(s) = \frac{\omega_n^2}{s^2 + \omega_n^2}
\end{align}
$$
Returning to the generic second order system, if $a\neq0$ there is some damping.
$$
G(s) = \frac{\omega_n^2}{s^2 + as + \omega_n^2}
$$
Poles are
$$
\begin{align}
s_p &= \frac{-a \pm \sqrt{a^2-4 \omega_n^2}}{2} \\
s_p &= -\frac{a}{2} \pm \frac{\sqrt{a^2-4 \omega_n^2}}{2} \\
\end{align}
$$
In the underdamped case, the poles contain both real and imaginary components. The poles then describe the impulse and step response as we saw previously. In that case, the real (decay) part is
$$
Re\{s_p\} = -\frac{a}{2}
$$
for both poles. As this real term describes the exponential decay, if we want a time scale agnostic variable $\zeta$ to describe the damping, we have
$$
\begin{align}
\zeta &= \frac{\text{Exponential Decay}}{\text{Natural Frequency}} \\
\zeta &= \frac{|-a/2|}{\omega_n} \\
\zeta &= \frac{a/2}{\omega_n} \\
a &= 2 \zeta \omega_n \\
\end{align}
$$
Underdamped Second Order System Magnitude
Recall that the system response magnitude may be described by
$$
\begin{align}
|H(j \omega)| &= b_0 \frac{\omega_n^2}{ \sqrt{(\omega_n^2 – \omega^2)^2 + (2 \zeta \omega_n \omega)^2}} \\
\end{align}
$$
To simplify this, we will use a new variable for convenience called $X$ where
$$
\begin{align}
X &= (\omega_n^2 – \omega^2)^2 + (2 \zeta \omega_n \omega)^2 \\
\\
|H(j \omega)| &= b_0 \frac{\omega_n^2}{\sqrt{X}} \\
\end{align}
$$
To find the frequency at which the maximum magnitude(s) occur, we must first find local maxima/minima. To do this, the local extrema must satisfy
$$
\begin{align}
0 &= \frac{d}{d \omega} |H(j \omega)| \\
0 &= \frac{\sqrt{X} \cdot 0 – b_0 \omega_n \frac{d}{d \omega} \sqrt{X}}{X} \\
0 &= \frac{- b_0 \omega_n \frac{d}{d \omega} \sqrt{X}}{X} \\
0 &= \frac{d}{d \omega} \sqrt{X} \\
0 &= \frac{1}{2} X^{-1/2} \frac{d}{d \omega} X \\
0 &= \frac{d}{d \omega} X \\
\end{align}
$$
Now we complete our usage of $X$ and substitute its original definition.
$$
\begin{align}
0 &= \frac{d}{d \omega} \left[ (\omega_n^2 – \omega^2)^2 + (2 \zeta \omega_n \omega)^2 \right] \\
0 &= 2 (\omega_n^2 – \omega^2) (-2 \omega) + 2 (2 \zeta \omega_n \omega) (2 \zeta \omega_n) \\
0 &= -4 \omega (\omega_n^2 – \omega^2) + 8 \omega (\zeta \omega_n)^2 \\
0 &= – (\omega_n^2 – \omega^2) + 2 (\zeta \omega_n)^2 &&\omega_{max} \neq 0 \\
0 &= \omega^2 – \omega_n^2 + 2 \zeta^2 \omega_n^2 &&\omega_{max} \neq 0 \\
0 &= \omega^2 – \omega_n^2(1 – 2 \zeta^2) &&\omega_{max} \neq 0 \\
\omega^2 &= \omega_n^2(1 – 2 \zeta^2) &&\omega_{max} \neq 0 \\
\omega &= \omega_n \sqrt{1 – 2 \zeta^2} &&\omega_{max} \neq 0 \\
\end{align}
$$
In summary we have found that there will be a peak in the frequency response at
$$
\begin{align}
\omega_{max} &= \omega_n \sqrt{1 – 2 \zeta^2} && \zeta < \frac{\sqrt{2}}{2} \\
\end{align}
$$
Note that in order for this peak to exist, we must meet the condition
$$
\begin{align}
1 – 2 \zeta^2 &> 0 \\
– 2 \zeta^2 &> -1 \\
\zeta^2 &< \frac{1}{2} \\
\zeta &< \frac{1}{\sqrt{2}} \\
\zeta &< \frac{\sqrt{2}}{2} \\
\end{align}
$$
Note that this is more restrictive than the condition for the system to be called underdamped ($\zeta < 1$). The magnitude at this peak is determined through substitution
$$
\begin{align}
\omega_{max} &= \omega_n \sqrt{1 – 2 \zeta^2} \\
\omega_{max}^2 &= \omega_n^2 (1 – 2 \zeta^2) \\
\\
|H(j \omega_{max})| &= b_0 \frac{\omega_n^2}{ \sqrt{[\omega_n^2 – \omega_{max}^2]^2 + [2 \zeta \omega_n \omega_{max}]^2}} \\
|H(j \omega_{max})| &= b_0 \frac{\omega_n^2}{ \sqrt{[\omega_n^2 – \omega_n^2 (1 – 2 \zeta^2)]^2 + [2 \zeta \omega_n (\omega_n \sqrt{1 – 2 \zeta^2})]^2}} \\
|H(j \omega_{max})| &= b_0 \frac{\omega_n^2}{ \sqrt{[\omega_n^2 – \omega_n^2 + 2 \zeta^2 \omega_n^2]^2 + [2 \zeta \omega_n^2 \sqrt{1 – 2 \zeta^2}]^2}} \\
|H(j \omega_{max})| &= b_0 \frac{\omega_n^2}{ \sqrt{[2 \zeta^2 \omega_n^2]^2 + [2 \zeta \omega_n^2]^2 (1 – 2 \zeta^2)}} \\
|H(j \omega_{max})| &= b_0 \frac{\omega_n^2}{ \sqrt{4 \zeta^4 \omega_n^4 + 4 \zeta^2 \omega_n^4 (1 – 2 \zeta^2)}} \\
|H(j \omega_{max})| &= b_0 \frac{\omega_n^2}{ \sqrt{(4 \omega_n^4 \zeta^2) [\zeta^2 + (1 – 2 \zeta^2)] } } \\
|H(j \omega_{max})| &= b_0 \frac{\omega_n^2}{ 2 \omega_n^2 \zeta \sqrt{1 – \zeta^2 } } \\
|H(j \omega_{max})| &= \frac{b_0}{ 2 \zeta \sqrt{1 – \zeta^2 } } \\
\end{align}
$$
If $\zeta > \frac{\sqrt{2}}{2}$ then the magnitude decreases monotonically from DC, and maximum magnitude occurs at $\omega=0$.
Underdamped Second Order System Bandwidth
In the case when $0 < \zeta < \frac{\sqrt{2}}{2}$, a peak occurs in the frequncy response. If we define the bandwidth as the region of frequencies such that $|H(j \omega)|^2 \geq \frac{1}{2} |H(j \omega_{max})|$ or $|H(j \omega)| \geq \frac{\sqrt{2}}{2} |H(j \omega_{max})|$ then we can use our previous derivation of magnitude to find at which points these occur. (added on analysis from approximation on pg 681). Recall that the magnitude may be expressed as
$$
|H(j \omega)| = b_0 \frac{\omega_n^2}{\sqrt{\omega_n^4 + \omega^4 + 2 \omega^2 \omega_n^2(2 \zeta^2 – 1)}} \\
$$
We then can find the bounds of the bandwidth as they occur when the following condition is met
$$
\begin{align}
b_0 \frac{\omega_n^2}{\sqrt{\omega_n^4 + \omega^4 + 2 \omega^2 \omega_n^2(2 \zeta^2 – 1)}} &= \frac{\sqrt{2}}{2} \frac{b_0}{ 2 \zeta \sqrt{ 1 – \zeta^2}} && \zeta < \frac{\sqrt{2}}{2} \\
\frac{\omega_n^2}{\sqrt{\omega_n^4 + \omega^4 + 2 \omega^2 \omega_n^2(2 \zeta^2 – 1)}} &= \frac{\sqrt{2}}{ 4 \zeta \sqrt{ 1 – \zeta^2}} && \zeta < \frac{\sqrt{2}}{2} \\
4 \zeta \omega_n^2 \sqrt{ 1 – \zeta^2} &= \sqrt{2} \sqrt{\omega_n^4 + \omega^4 + 2 \omega^2 \omega_n^2(2 \zeta^2 – 1)} && \zeta < \frac{\sqrt{2}}{2} \\
16 \zeta^2 \omega_n^4 (1 – \zeta^2) &= 2 [\omega_n^4 + \omega^4 + 2 \omega^2 \omega_n^2(2 \zeta^2 – 1)] && \zeta < \frac{\sqrt{2}}{2} \\
8 \zeta^2 \omega_n^4 (1 – \zeta^2) &= \omega_n^4 + \omega^4 + 2 \omega^2 \omega_n^2(2 \zeta^2 – 1) && \zeta < \frac{\sqrt{2}}{2} \\
0 &= \omega^4 + \omega^2 [2 \omega_n^2(2 \zeta^2 – 1)] + [\omega_n^4 – 8 \zeta^2 \omega_n^4 (1 – \zeta^2)] && \zeta < \frac{\sqrt{2}}{2} \\
0 &= \omega^4 + \omega^2 [2 \omega_n^2(2 \zeta^2 – 1)] + \omega_n^4[1 – 8 \zeta^2 (1 – \zeta^2)] && \zeta < \frac{\sqrt{2}}{2} \\
\end{align}
$$
Using quadratic equation
$$
\begin{align}
\omega^2 &= \frac{- 2 \omega_n^2(2 \zeta^2 – 1) \pm \sqrt{[2 \omega_n^2(2 \zeta^2 – 1)]^2 – 4 \omega_n^4[1 – 8 \zeta^2 (1 – \zeta^2)]}}{2} && \zeta < \frac{\sqrt{2}}{2} \\
\omega^2 &= \frac{1}{2} \left[- 2 \omega_n^2(2 \zeta^2 – 1) \pm \sqrt{[2 \omega_n^2(2 \zeta^2 – 1)]^2 – 4 \omega_n^4[1 – 8 \zeta^2 (1 – \zeta^2)]} \right] && \zeta < \frac{\sqrt{2}}{2} \\
\omega_2 &= \frac{1}{2} \left[- 2 \omega_n^2(2 \zeta^2 – 1) \pm \sqrt{4 \omega_n^4 (2 \zeta^2 – 1)^2 – 4 \omega_n^4[1 – 8 \zeta^2 (1 – \zeta^2)]} \right] && \zeta < \frac{\sqrt{2}}{2} \\
\omega^2 &= \frac{1}{2} \left[- 2 \omega_n^2(2 \zeta^2 – 1) \pm 2 \omega_n^2 \sqrt{(2 \zeta^2 – 1)^2 – [1 – 8 \zeta^2 (1 – \zeta^2)]} \right] && \zeta < \frac{\sqrt{2}}{2} \\
\omega^2 &= \omega_n^2 \left[ – (2 \zeta^2 – 1) \pm \sqrt{(2 \zeta^2 – 1)^2 – [1 – 8 \zeta^2 (1 – \zeta^2)]} \right] && \zeta < \frac{\sqrt{2}}{2} \\
\omega^2 &= \omega_n^2 \left[ 1 – 2 \zeta^2 \pm \sqrt{4 \zeta^4 – 4 \zeta^2 + 1 – [1 – 8 \zeta^2 + 8 \zeta^4]} \right] && \zeta < \frac{\sqrt{2}}{2} \\
\omega^2 &= \omega_n^2 \left[ 1 – 2 \zeta^2 \pm \sqrt{4 \zeta^4 – 4 \zeta^2 + 1 – 1 + 8 \zeta^2 – 8 \zeta^4} \right] && \zeta < \frac{\sqrt{2}}{2} \\
\omega^2 &= \omega_n^2 \left[ 1 – 2 \zeta^2 \pm \sqrt{4 \zeta^2 – 4 \zeta^4} \right] && \zeta < \frac{\sqrt{2}}{2} \\
\omega^2 &= \omega_n^2 \left[ 1 – 2 \zeta^2 \pm 2 \zeta^2 \sqrt{1 – \zeta^2} \right] && \zeta < \frac{\sqrt{2}}{2} \\
\omega^2 &= \omega_n^2 \left[ 1 – 2 \zeta^2 \left( 1 \pm \sqrt{1 – \zeta^2} \right) \right] && \zeta < \frac{\sqrt{2}}{2} \\
\omega^2 &= \omega_n^2 – 2 \omega_n^2 \zeta^2 \left( 1 \pm \sqrt{1 – \zeta^2} \right) && \zeta < \frac{\sqrt{2}}{2} \\
\end{align}
$$
If $\omega$ and $\omega_n$ are assumed same sign (positive), we have
$$
\begin{align}
\omega_{BW} &= \omega_n \sqrt{ 1 – 2 \zeta^2 \pm 2 \zeta^2 \sqrt{1 – \zeta^2}} && \zeta < \frac{\sqrt{2}}{2} \\
\\
\omega_{BW} &= \omega_n \frac{\sqrt{1-2\zeta^2}}{\sqrt{1-2\zeta^2}} \sqrt{ 1 – 2 \zeta^2 \pm 2 \zeta^2 \sqrt{1 – \zeta^2}} && \zeta < \frac{\sqrt{2}}{2} \\
\\
\omega_{BW} &= \omega_n \sqrt{1-2\zeta^2} \sqrt{ \frac{1 – 2 \zeta^2 \pm 2 \zeta^2 \sqrt{1 – \zeta^2}}{1-2\zeta^2}} && \zeta < \frac{\sqrt{2}}{2} \\
\\
\omega_{BW} &= \omega_n \sqrt{1-2\zeta^2} \sqrt{ 1 \pm \frac{2 \zeta^2}{1-2\zeta^2} \sqrt{1 – \zeta^2}} && \zeta < \frac{\sqrt{2}}{2} \\
\\
\omega_{BW} &= \omega_{max} \sqrt{ 1 \pm \frac{2 \zeta^2}{1-2\zeta^2} \sqrt{1 – \zeta^2}} && \zeta < \frac{\sqrt{2}}{2} \\
\end{align}
$$
Note that as $\zeta \to \frac{\sqrt{2}}{2}$ the denominator approaches 0, the terms to the right of the $\pm$ approach infinity, and therefore, the bandwidth widens. On the other hand as $\zeta \to 0$, the numerator approaches 0 and the bandwidth narrows.
Underdamped Second Order System Peak Time, $T_p$
Time required to reach first (maximum) peak is found by differentiating step response signal with respect to time and finding first zero. Assuming initial conditions at rest,
$$
\begin{align}
\mathscr{L}[\dot{s}(t)] &= s S(s) \\
\mathscr{L}[\dot{s}(t)] &= \frac{\omega_n^2}{s^2 + 2 \zeta \omega_n s + \omega_n^2} \\
\mathscr{L}[\dot{s}(t)] &= \frac{\omega_n^2}{s^2 + 2 \zeta \omega_n s + (\zeta \omega_n)^2 – (\zeta \omega_n)^2 + \omega_n^2} \\
\mathscr{L}[\dot{s}(t)] &= \frac{\omega_n^2}{(s + \zeta \omega_n)^2 + \omega_n^2- \zeta^2 \omega_n^2} \\
\mathscr{L}[\dot{s}(t)] &= \frac{\omega_n^2}{(s + \zeta \omega_n)^2 + \omega_n^2(1- \zeta^2)} \\
\end{align}
$$
Recall that
$$
\begin{align}
\sin(\omega_0 t) u(t) &\stackrel{\mathscr{L}}{\leftrightarrow} \frac{\omega_0}{s^2 + \omega_0^2} && Re\{s\} > 0 \\
\\
e^{s_0 t} x(t) &\stackrel{\mathscr{L}}{\leftrightarrow} X(s-s_0) &&ROC: Re\{s\} \in R + Re\{s_0\} \\
\end{align}
$$
So let’s do some rearranging to get to a more usable form
$$
\begin{align}
\mathscr{L}[\dot{s}(t)] &= \frac{\omega_n^2}{(s + \zeta \omega_n)^2 + (\omega_n \sqrt{1- \zeta^2})^2} \\
\mathscr{L}[\dot{s}(t)] &= \omega_n \frac{ \omega_n }{(s + \zeta \omega_n)^2 + (\omega_n \sqrt{1- \zeta^2})^2} \\
\mathscr{L}[\dot{s}(t)] &= \frac{\omega_n}{\sqrt{1- \zeta^2}} \frac{ \omega_n \sqrt{1- \zeta^2} }{(s + \zeta \omega_n)^2 + (\omega_n \sqrt{1- \zeta^2})^2} \\
\end{align}
$$
Now we can move through the relevant transforms in slow motion to find the resulting equation
$$
\begin{align}
\sin(\omega_n \sqrt{1 – \zeta^2} t) u(t) &\stackrel{\mathscr{L}}{\leftrightarrow} \frac{ \omega_n \sqrt{1- \zeta^2} }{s^2 + (\omega_n \sqrt{1- \zeta^2})^2} \\
\\
s – s_0 &= s + \zeta \omega_n\\
s_0 &= -\zeta \omega_n\\
e^{- \zeta \omega_n} \sin(\omega_n \sqrt{1 – \zeta^2} t) u(t) &\stackrel{\mathscr{L}}{\leftrightarrow} \frac{ \omega_n \sqrt{1- \zeta^2} }{(s + \zeta \omega_n)^2 + (\omega_n \sqrt{1- \zeta^2})^2} \\
\\
\frac{\omega_n}{\sqrt{1- \zeta^2}} e^{- \zeta \omega_n} \sin(\omega_n \sqrt{1 – \zeta^2} t) u(t) &\stackrel{\mathscr{L}}{\leftrightarrow} \frac{\omega_n}{\sqrt{1- \zeta^2}} \frac{ \omega_n \sqrt{1- \zeta^2} }{(s + \zeta \omega_n)^2 + (\omega_n \sqrt{1- \zeta^2})^2} \\
\end{align}
$$
so the first derivative of the step response to an underdamped lowpass system is
$$
\dot{s}(t) = \frac{\omega_n}{\sqrt{1- \zeta^2}} e^{- \zeta \omega_n} \sin(\omega_n \sqrt{1 – \zeta^2} t) u(t) \\
$$
This result is zero only when
$$
\begin{align}
\sin(\omega_n \sqrt{1 – \zeta^2} t) &= 0 && t > 0 \\
\omega_n \sqrt{1 – \zeta^2} t &= n \pi && t > 0, n \in \mathbb{Z}, n > 0 \\
t &= \frac{n \pi}{\omega_n \sqrt{1 – \zeta^2}} && t > 0, n \in \mathbb{Z}, n > 0 \\
\end{align}
$$
First peak occurs when $n = 1$ or at
$$
T_p = \frac{\pi}{\omega_n \sqrt{1 – \zeta^2}} \\
$$
Underdamped Second Order System Percent Overshoot, %OS
Amount in percentage that waveform overshoots the steady state value.
$$
\begin{align}
\%OS &= \frac{s(T_p) – s(\infty)}{s(\infty)} \cdot 100 \\
\%OS &= \frac{s(T_p) – b_0}{b_0} \cdot 100 \\
\end{align}
$$
$s(T_p)$ can be found from the underdamped step response.
$$
\begin{align}
T_p &= \frac{\pi}{\omega_n \sqrt{1 – \zeta^2}} \\
\\
s(T_p) &= b_0 \left\{1 – e^{-\zeta\omega_n T_p} \left[ \cos(\omega_n \sqrt{1 – \zeta^2}T_p) + \frac{\zeta}{\sqrt{1-\zeta^2}} \sin(\omega_n \sqrt{1-\zeta^2} T_p) \right] \right\} \\
s(T_p) &= b_0 \left\{1 – e^{-(\pi \zeta / \sqrt{1-\zeta^2})} \left[ \cos(\pi) + \frac{\zeta}{\sqrt{1-\zeta^2}} \sin(\pi) \right] \right\} \\
s(T_p) &= b_0 \left\{1 – e^{-(\pi \zeta / \sqrt{1-\zeta^2})} \left[ -1 + 0 \right]\right\} \\
s(T_p) &= b_0 \left\{1 + e^{-(\pi \zeta / \sqrt{1-\zeta^2})} \right\} \\
s(T_p) &= b_0 + b_0 e^{-(\pi \zeta / \sqrt{1-\zeta^2})} \\
\end{align}
$$
So finally returning to the %OS equation
$$
\begin{align}
\%OS &= \frac{b_0 + b_0 e^{-(\pi \zeta / \sqrt{1-\zeta^2})} – b_0}{b_0} \cdot 100 \\
\%OS &= \frac{b_0 e^{-(\pi \zeta / \sqrt{1-\zeta^2})}}{b_0} \cdot 100 \\
\%OS &= e^{-(\pi \zeta / \sqrt{1-\zeta^2})} \cdot 100 \\
\end{align}
$$
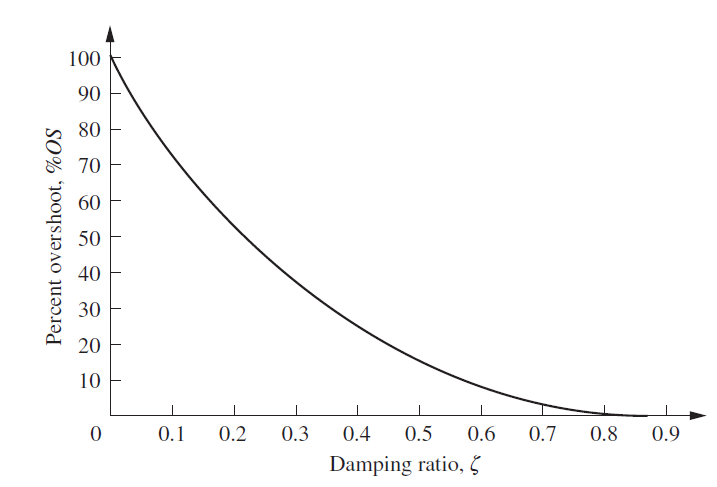
Note that this result is independent of the scaling of the step input and only a function of the damping ratio. This means we can solve for $\zeta$ based on a desired overshoot.
$$
\begin{align}
\frac{\%OS}{100} = e^{-(\pi \zeta / \sqrt{1-\zeta^2})} \\
\ln \left(\frac{\%OS}{100}\right) = -\frac{\pi \zeta}{\sqrt{1-\zeta^2}} \\
-\frac{1}{\pi} \ln \left(\frac{\%OS}{100}\right) = \frac{\zeta}{\sqrt{1-\zeta^2}} \\
\end{align}
$$
Note that if we have
$$
A = \frac{\zeta}{\sqrt{1-\zeta^2}} \\
$$
then $\zeta$ and $A$ must be the same sign. Additionally
$$
\begin{align}
A \sqrt{1-\zeta^2} &= \zeta \\
\sqrt{A^2-\zeta^2 A^2} &= \zeta \\
A^2-\zeta^2 A^2 &= \zeta^2 \\
A^2 &= \zeta^2 (1 + A^2) \\
\zeta^2 &= \frac{A^2}{1 + A^2} \\
\zeta &= \frac{A}{ \sqrt{1 + A^2}} \\
\end{align}
$$
So if we define
$$
\begin{align}
A &= -\frac{1}{\pi} \ln \left(\frac{\%OS}{100}\right) \\
A^2 &= \frac{1}{\pi^2} \ln^2 \left(\frac{\%OS}{100}\right) \\
\end{align}
$$
then
$$
\begin{align}
\zeta &= \frac{-\frac{1}{\pi} \ln \left(\frac{\%OS}{100}\right)}{ \sqrt{1 + \frac{1}{\pi^2} \ln^2 \left(\frac{\%OS}{100}\right)}} \\
\zeta &= \frac{- \ln \left(\frac{\%OS}{100}\right)}{ \pi \sqrt{1 + \frac{1}{\pi^2} \ln^2 \left(\frac{\%OS}{100}\right)}} \\
\zeta &= \frac{- \ln \left(\frac{\%OS}{100}\right)}{\sqrt{\pi^2 + \ln^2 \left(\frac{\%OS}{100}\right)}} \\
\end{align}
$$
Underdamped Second Order System Settling Time, $T_s$
Settling time is the required time for damped oscillations to stay within some percent $p$ of final value. Recall from the underdamped step response
$$
s(t) = b_0 u(t) \left\{1 – e^{-\zeta\omega_n t} \sqrt{\frac{1}{1 – \zeta^2}} \cos\left[ \omega_n\sqrt{1-\zeta^2}t – \tan^{-1}\left(\frac{\zeta}{\sqrt{1 – \zeta^2}}\right) \right] \right\} \\
$$
Which shows that the amplitude of the sinusoidal component will be $pb_0$ when
$$
\begin{align}
b_0 e^{-\zeta \omega_n T_s} \sqrt{\frac{1}{1-\zeta^2}} &= b_0 p \\
e^{-\zeta \omega_n T_s} \sqrt{\frac{1}{1-\zeta^2}} &= p \\
e^{-\zeta \omega_n T_s} &= p \sqrt{1-\zeta^2} \\
-\zeta \omega_n T_s &= \ln(p \sqrt{1-\zeta^2}) \\
T_s &= \frac{-\ln(p \sqrt{1-\zeta^2})}{\zeta \omega_n} \\
\end{align}
$$
When $p=0.02$, then the numerator varies around roughly $4$ as $\zeta \in [0,0.9]$, so a common approximation used is
$$
T_s \approx \frac{4}{\zeta \omega_n}
$$
For reference, this approximation corresponds to the case when
$$
\begin{align}
-\ln(p \sqrt{1-\zeta^2}) &= 4 &&T_s = \frac{4}{\zeta \omega_n} \\
\ln(p \sqrt{1-\zeta^2}) &= -4 &&T_s = \frac{4}{\zeta \omega_n} \\
p \sqrt{1-\zeta^2} &= e^{-4} &&T_s = \frac{4}{\zeta \omega_n} \\
\sqrt{1-\zeta^2} &= \frac{e^{-4}}{p} &&T_s = \frac{4}{\zeta \omega_n} \\
1-\zeta^2 &= \frac{e^{-8}}{p^2} &&T_s = \frac{4}{\zeta \omega_n} \\
\zeta &= \sqrt{1 – \frac{e^{-8}}{p^2}} &&T_s = \frac{4}{\zeta \omega_n} \\
\zeta &\approx 0.4 &&T_s = \frac{4}{\zeta \omega_n}, p = 0.02 \\
\end{align}
$$
Underdamped Second Order System Rise Time $T_r$
Time required for waveform to go from 10% final value to 90% final value. This cannot be solved analytically for a specific $\zeta$, but can be solved numerically using $\omega_n T_r$, a normalized rise time.
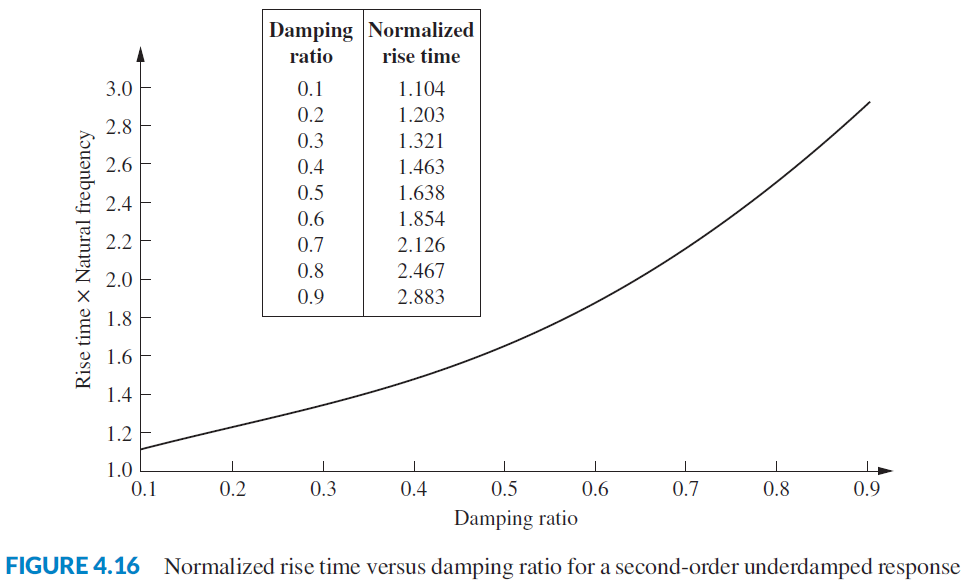
Underdamped Second Order System Graphical Representation of System Parameters
Real and imaginary parts of poles of underdamped system may be expressed from
$$
\begin{align}
c_1 = -\zeta \omega_n + \omega_n j\sqrt{1-\zeta^2} \\
c_2 = -\zeta \omega_n – \omega_n j\sqrt{1-\zeta^2} \\
\end{align}
$$
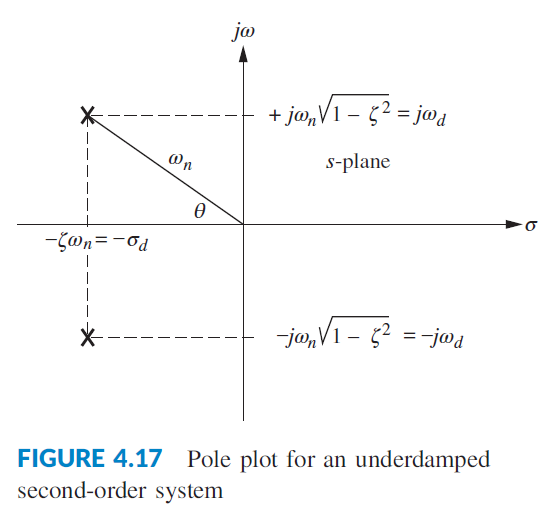
So we may also realize that:
$$
\begin{align}
T_s \approx \frac{4}{\zeta \omega_n} \\
Re\{c_1, c_2\} = -\zeta \omega_n \\
\end{align}
$$
Vertical motion of a pole corresponds to maintaining a constant settle time (both $T_s$ and $\zeta \omega_n$ are preserved).
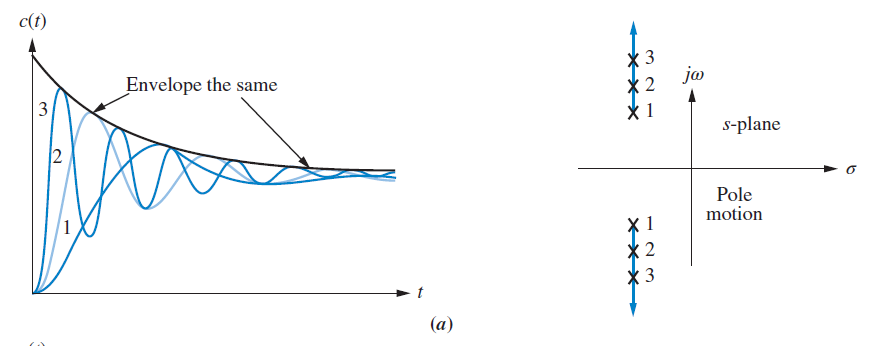
$$
\begin{align}
T_p &= \frac{\pi}{\omega_n \sqrt{1 – \zeta^2}} \\
|Im\{c_1, c_2\}| &= j \omega_n \sqrt{1-\zeta^2} \\
\end{align}
$$
Horizontal motion of a pole corresponds to maintaining a constant peak time (both $T_p$ and $\omega_n \sqrt{1 – \zeta^2}$ are preserved)
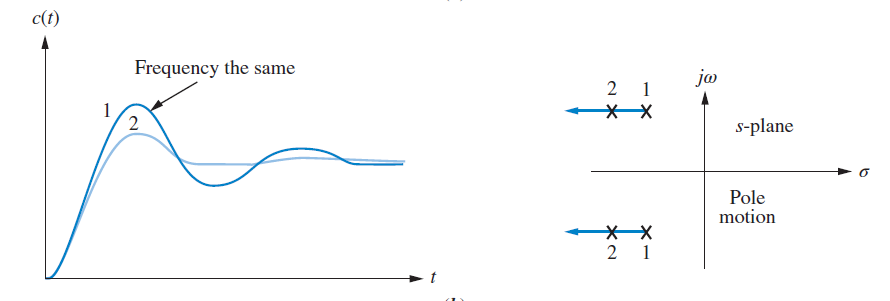
$$
\begin{align}
\%OS &= e^{-(\pi \zeta / \sqrt{1-\zeta^2})} \cdot 100 \\
\pi – \angle c_1 &= \tan^{-1} \left( \frac{\omega_n \sqrt{1 – \zeta^2}}{\zeta \omega_n} \right) &= \tan^{-1} \left( \frac{\sqrt{1 – \zeta^2}}{\zeta} \right) \\
\end{align}
$$
Motion along the same angle from the origin corresponds to a constant overshoot (%OS, $\zeta$, and $\zeta/\sqrt{1 – \zeta^2}$ are all preserved). Shallower angle corresponds to smaller fraction in $\tan^{-1}$ function, which means larger value in parentheses of exponential, which means less overshoot. This makes intuitive sense as this means the poles approach the critically damped condition.
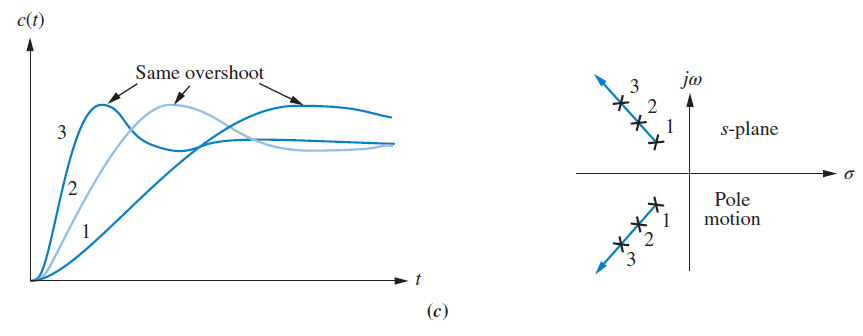
Underdamped Second Order System Bandpass
$$
\begin{align}
|H(j \omega)| &= \left| \frac{j\omega}{(j \omega)^2 + 2 \zeta \omega_n (j \omega) + \omega_n^2} \right| \\
|H(j \omega)| &= \frac{\omega}{ | \omega_n^2 – \omega^2 + j 2 \zeta \omega_n \omega |} \\
|H(j \omega)| &= \frac{\omega}{ \sqrt{(\omega_n^2 – \omega^2)^2 + (2 \zeta \omega_n \omega)^2}} \\
\end{align}
$$
To find the magnitude maximum, we can use similar analysis as in the lowpass case. We will again use a convenience variable, $X$
$$
\begin{align}
X &= (\omega_n^2 – \omega^2)^2 + (2 \zeta \omega_n \omega)^2 \\
\\
|H(j \omega)| &= \frac{\omega}{ \sqrt{X} } \\
\end{align}
$$
Local extrema must then satisfy
$$
\begin{align}
0 &= \frac{d}{d \omega} |H(j \omega)| \\
0 &= \frac{d}{d \omega} \frac{\omega}{ \sqrt{X} } \\
0 &= \frac{\sqrt{X} \cdot 1 – \omega \frac{d}{d \omega} \sqrt{X}}{ X } \\
0 &= \frac{X^{1/2} – \omega \frac{1}{2} X^{-1/2} \frac{d}{d \omega} X}{ X } \\
0 &= X^{1/2} – \omega \frac{1}{2} X^{-1/2} \frac{d}{d \omega} X \\
X^{1/2} &= \frac{\omega}{2} X^{-1/2} \frac{d}{d \omega} X \\
X &= \frac{\omega}{2} \frac{d}{d \omega} X \\
(\omega_n^2 – \omega^2)^2 + (2 \zeta \omega_n \omega)^2 &= \frac{\omega}{2} \frac{d}{d \omega} [(\omega_n^2 – \omega^2)^2 + (2 \zeta \omega_n \omega)^2] \\
(\omega_n^2 – \omega^2)^2 + (2 \zeta \omega_n \omega)^2 &= \frac{\omega}{2} [2(\omega_n^2 – \omega^2)(-2 \omega) + 2(2 \zeta \omega_n \omega)(2 \zeta \omega_n)] \\
(\omega_n^2 – \omega^2)^2 + (2 \zeta \omega_n \omega)^2 &= -2 \omega^2 (\omega_n^2 – \omega^2) + (2 \zeta \omega_n \omega)(2 \zeta \omega_n \omega) \\
(\omega_n^2 – \omega^2)^2 + (2 \zeta \omega_n \omega)^2 &= -2 \omega^2 (\omega_n^2 – \omega^2) + (2 \zeta \omega_n \omega)^2 \\
(\omega_n^2 – \omega^2)^2 + 2 \omega^2 (\omega_n^2 – \omega^2) &= 0 \\
(\omega_n^2 – \omega^2)[(\omega_n^2 – \omega^2) + 2 \omega^2] &= 0 \\
(\omega_n^2 – \omega^2)(\omega_n^2 + \omega^2) &= 0 \\
\omega &= \omega_n
\end{align}
$$
In summary as expected, the peak for a second order bandpass filter occurs when $\omega = \omega_n$. Magnitude at this frequency is
$$
\begin{align}
|H(j \omega)|_{\omega = \omega_n} &= \frac{\omega_n}{ \sqrt{(\omega_n^2 – \omega_n^2)^2 + (2 \zeta \omega_n \omega_n)^2}} \\
|H(j \omega)|_{\omega = \omega_n} &= \frac{\omega_n}{2 \zeta \omega_n^2} \\
|H(j \omega)|_{\omega = \omega_n} &= \frac{1}{2 \zeta \omega_n} \\
\end{align}
$$
Comparison to Cascaded First Order HPF and LPF
A first order lowpass and first order highpass system in series would have the frequency response
$$
\begin{align}
H(s) &= \left( \frac{1}{\tau_{lpf} s + 1} \right) \left( \frac{\tau_{hpf} s}{\tau_{hpf} s + 1} \right) \\
H(s) &= \frac{\tau_{hpf} s}{\tau_{hpf} \tau_{lpf} s^2 + (\tau_{hpf} + \tau_{lpf}) s + 1} \\
\end{align}
$$
Rearranging this equation to resemble the more common form found above we have
$$
\begin{align}
H(s) &= \frac{\tau_{hpf}}{\tau_{lpf}} \frac{ s }{s^2 + \frac{\tau_{hpf} + \tau_{lpf}}{\tau_{hpf} \tau_{lpf}} s + \frac{1}{\tau_{hpf} \tau_{lpf}}} \\
\\
\omega_n^2 &= \frac{1}{ \tau_{hpf} \tau_{lpf} } \\
\omega_n &= \frac{1}{ \sqrt{ \tau_{hpf} \tau_{lpf} } } \\
\\
2 \zeta \omega_n &= \frac{ \tau_{hpf} + \tau_{lpf} }{ \tau_{hpf} \tau_{lpf} } \\
2 \zeta \frac{1}{ \sqrt{ \tau_{hpf} \tau_{lpf} } } &= \frac{ \tau_{hpf} + \tau_{lpf} }{ \tau_{hpf} \tau_{lpf} } \\
\zeta &= \frac{ \sqrt{ \tau_{hpf} \tau_{lpf} } ( \tau_{hpf} + \tau_{lpf} ) }{ 2 \tau_{hpf} \tau_{lpf} } \\
\zeta &= \frac{1}{2} \frac{ \tau_{hpf} + \tau_{lpf} }{ \sqrt{ \tau_{hpf} \tau_{lpf} } } \\
\end{align}
$$
Or using $\tau = 1 / \omega_0$
$$
\begin{align}
H(s) &= \frac{1 / \omega_{hpf}}{1 / \omega_{lpf}} \frac{ s }{s^2 + \frac{(1 / \omega_{hpf}) + (1 / \omega_{lpf})}{(1 / \omega_{hpf}) (1 / \omega_{lpf})} s + \frac{1}{(1 / \omega_{hpf}) (1 / \omega_{lpf})}} \\
H(s) &= \frac{ \omega_{lpf} }{ \omega_{hpf} } \frac{ s }{s^2 + \omega_{hpf} \omega_{lpf} \left( \frac{1}{\omega_{hpf}} + \frac{1}{\omega_{lpf}} \right) s + \omega_{hpf} \omega_{lpf} } \\
H(s) &= \frac{ \omega_{lpf} }{ \omega_{hpf} } \frac{ s }{s^2 + (\omega_{hpf} + \omega_{lpf}) s + \omega_{hpf} \omega_{lpf} } \\
\\
\omega_n^2 &= \omega_{hpf} \omega_{lpf} \\
\omega_n &= \sqrt{ \omega_{hpf} \omega_{lpf} } \\
\\
2 \zeta \omega_n &= \omega_{hpf} + \omega_{lpf} \\
2 \zeta \sqrt{ \omega_{hpf} \omega_{lpf} } &= \omega_{hpf} + \omega_{lpf} \\
\zeta &= \frac{1}{2} \frac{ \omega_{hpf} + \omega_{lpf} }{ \sqrt{ \omega_{hpf} \omega_{lpf} } } \\
\end{align}
$$
Critically Damped Second Order Systems, $\zeta = 1$ (and $c_1 = c_2$)
Fastest rise time in step response without overshoot.
$$
\begin{align}
c_1 = c_2 = – \omega_n \\
\\
H(j \omega) = b_0 \frac{\omega_n^2}{(j \omega + \omega_n)^2} \\
\end{align}
$$
Critically Damped Second Order System Impulse Response
From table
$$
h(t) = b_0 \omega_n^2 t e^{-\omega_n t} u(t)
$$
Critically Damped Second Order System Step Response
$$
\begin{align}
s(t) &= \int_{-\infty}^t h(x) dx \\
s(t) &= \int_{-\infty}^t b_0 \omega_n^2 x e^{-\omega_n x} u(x) dx \\
s(t) &= b_0 \omega_n^2 \int_{-\infty}^t x e^{-\omega_n x} u(x) dx \\
s(t) &= b_0 \omega_n^2 u(t) \int_{0}^t x e^{-\omega_n x} dx \\
\end{align}
$$
Using IBP
$$
\begin{align}
[f(x) g(x)]’ &= f'(x) g(x) + f(x) g'(x) \\
f(x) g'(x) &= [f(x) g(x)]’ – f'(x) g(x) \\
\int_a^b f(x) g'(x) dx &= \left[ f(x) g(x) \right]_a^b – \int_a^b f'(x) g(x) dx \\
\\
f(x) &= x \\
g'(x) &= e^{-\omega_n x} \\
\\
f'(x) &= 1 \\
g(x) &= -\frac{1}{\omega_n} e^{-\omega_n x} \\
\end{align}
$$
and so
$$
\begin{align}
\int_{0}^t x e^{-\omega_n x} dx &= \left[ -\frac{x}{\omega_n} e^{- \omega_n x} \right]_{x=0}^t – \int_0^t – \frac{1}{\omega_n} e^{- \omega_n x} dx \\
\int_{0}^t x e^{-\omega_n x} dx &= -\frac{1}{\omega_n} \left[ x e^{- \omega_n x} \right]_{x=0}^t + \frac{1}{\omega_n} \int_0^t e^{- \omega_n x} dx \\
\int_{0}^t x e^{-\omega_n x} dx &= -\frac{1}{\omega_n} \left[ x e^{- \omega_n x} \right]_{x=0}^t + \frac{1}{\omega_n} \left[ -\frac{1}{\omega_n} e^{- \omega_n x} \right]_{x=0}^t \\
\int_{0}^t x e^{-\omega_n x} dx &= -\frac{1}{\omega_n} \left[ x e^{- \omega_n x} \right]_{x=0}^t – \frac{1}{\omega_n^2} \left[ e^{- \omega_n x} \right]_{x=0}^t \\
\int_{0}^t x e^{-\omega_n x} dx &= -\frac{1}{\omega_n} \left[ t e^{- \omega_n t} \right] – \frac{1}{\omega_n^2} \left[ e^{- \omega_n t} – 1 \right] \\
\int_{0}^t x e^{-\omega_n x} dx &= -\frac{1}{\omega_n^2} \left[ \omega_n t e^{- \omega_n t} \right] – \frac{1}{\omega_n^2} \left[ e^{- \omega_n t} – 1 \right] \\
\int_{0}^t x e^{-\omega_n x} dx &= -\frac{1}{\omega_n^2} \left[ \omega_n t e^{- \omega_n t} + e^{- \omega_n t} – 1 \right] \\
\int_{0}^t x e^{-\omega_n x} dx &= \frac{1}{\omega_n^2} \left[ 1 – e^{- \omega_n t} -\omega_n t e^{- \omega_n t} \right] \\
\end{align}
$$
So the step function becomes
$$
\begin{align}
s(t) &= b_0 \omega_n^2 u(t) \left\{ \frac{1}{\omega_n^2} \left[ 1 – e^{- \omega_n t} -\omega_n t e^{- \omega_n t} \right] \right\} \\
s(t) &= b_0 \left[ 1 – e^{- \omega_n t} -\omega_n t e^{- \omega_n t} \right] u(t) \\
\end{align}
$$
Whew!