Geometric Interpretation of Complex Transforms

For rational transforms, there are various interpretations that can be visualized by plotting zeros and poles on the complex plane.

Vector Algebra Refresher

Recall from vector algebra, the difference between two vectors can be represented by the vector drawn from the subtrahend (second vector) to the minuend (first vector).

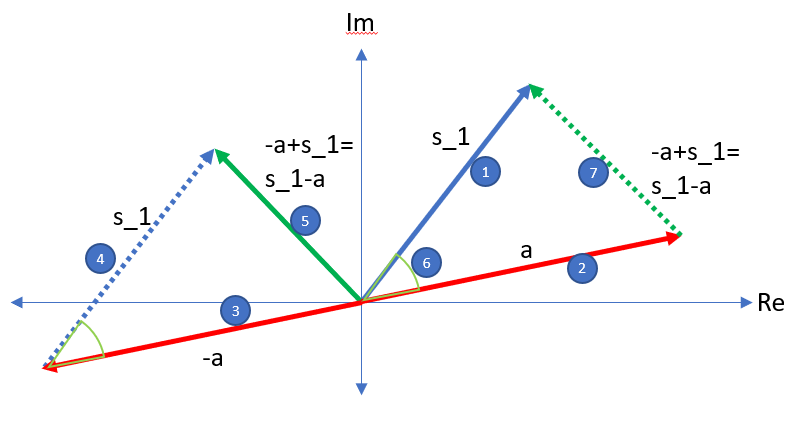
1. Draw minuend (first term)
2. Draw subtrahend (second term)
3. Draw inverse of subtrahend
4. Add minuend vector to inverted subtrahend vector.
5. The vector drawn from the origin to this location is the difference vector.
6. Because magnitude of inverted subtrahend and subtrahend are the same, we can apply Side-Angle-Side rule to confirm that triangle is fully defined.
7. Draw vector from subtrahend to minuend and prove that the vector is equivalent to the difference vector because triangles are equivalent.

Geometric Representation of Laplace Transforms

Now we can generalize for the poles $\phi$ and zeros $\zeta$ of a Laplace transform when evaluating for any $s$. A rational transform $X(s)$ may be generalized as a ratio of products.

$$
\begin{align}
X(s) &= M \frac{\prod_k s-\zeta_k}{\prod_r s-\phi_r} \\
\end{align}
$$

The magnitude of the signal evaluated at any $s$ may then be determined from

$$
\begin{align}
|X(s)| &= M \left| \frac{\prod_k s-\zeta_k}{\prod_r s-\phi_r} \right| \\
|X(s)| &= M \frac{\prod_k |s-\zeta_k|}{\prod_r |s-\phi_r|} \\
\end{align}
$$

and the phase angle is

$$
\begin{align}
\angle X(s) &= \angle \left[ M \frac{\prod_k s-\zeta_k}{\prod_r s-\phi_r} \right] \\
\end{align}
$$

$$
\angle X(s) = \cases{
\begin{align}
&\sum_k \angle(s-\zeta_k) – \sum_r \angle(s-\phi_r) && M > 0 \\
&\sum_k \angle(s-\zeta_k) – \sum_r \angle(s-\phi_r) + \pi && M < 0 \\
&0 &&M=0
\end{align}
}
$$

In other words, if one were to draw vectors from each pole and each zero to some specific $s_1$

1. The magnitude of $X(s_1)$ is the product of the magnitude of all vectors from zeros to $s_1$ divided by the product of all vectors from the poles to $s_1$.
2. The phase angle of $X(s_1)$ is evaluated by adding all vector angles from the zeros to $s_1$ and subtracting angles from poles to $s_1$. Note that if $M$ is negative, an additional angle of $\pi$ needs to be added to the angle to invert its direction.